Comment se protéger du piratage informatique
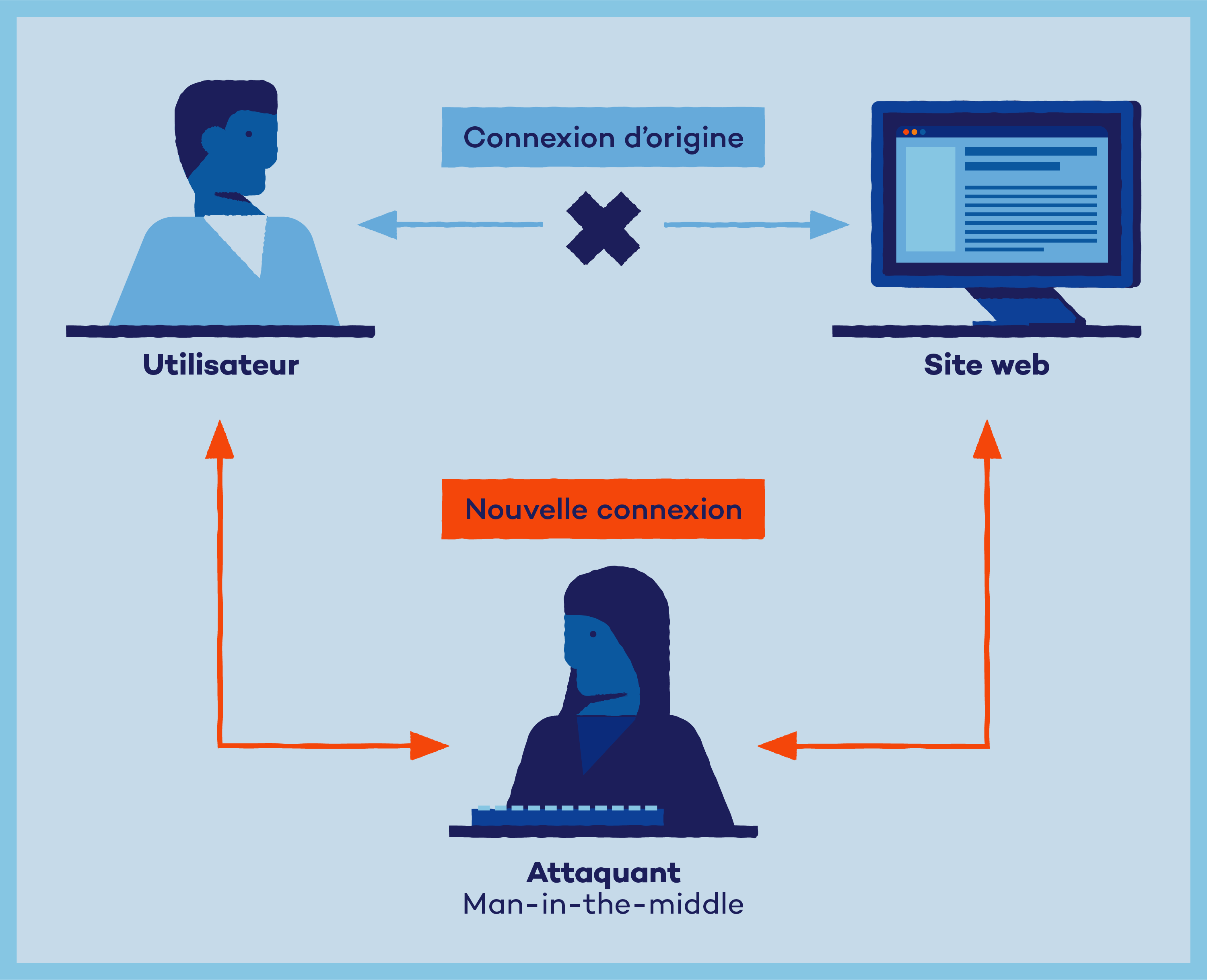

Le cryptage
Symétrique / Asymétrique
Cryptage symétrique
Symétrique
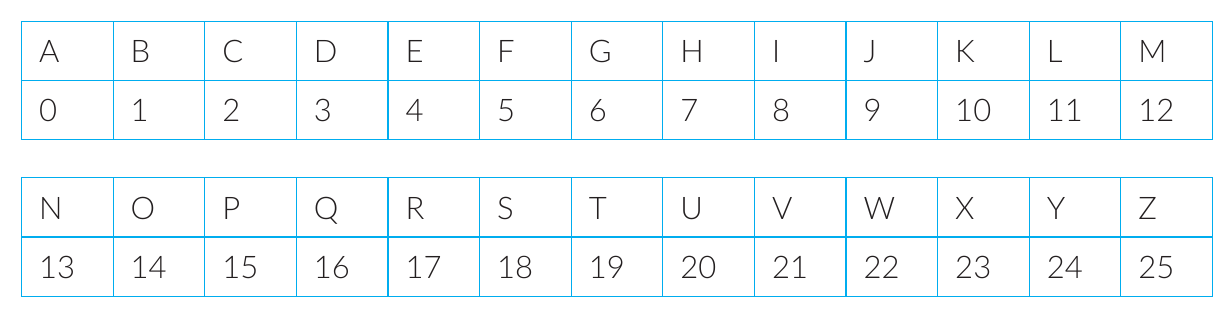
Le chiffrement de Vigenère introduit le principe de clé se présentant généralement sous la forme d’un mot (ou d’une phrase) que l’on répète. Plus la clé est longue et variée, mieux le texte sera chiffré.On considère la méthode de chiffrement suivante. À chaque lettre de l’alphabet, on fait correspondre sa position dans l’alphabet, c’est-à-dire un entier entre 0 et 25 (A correspondant à 0, B à 1, etc.)
À chaque lettre à coder, on associe l’entier x correspondant. À chaque lettre de la clé, on associe l’entier y correspondant. On détermine l’entier z , où z est le reste de x + y dans la division euclidienne par 26. La lettre chiffrée sera obtenue avec le nombre z .
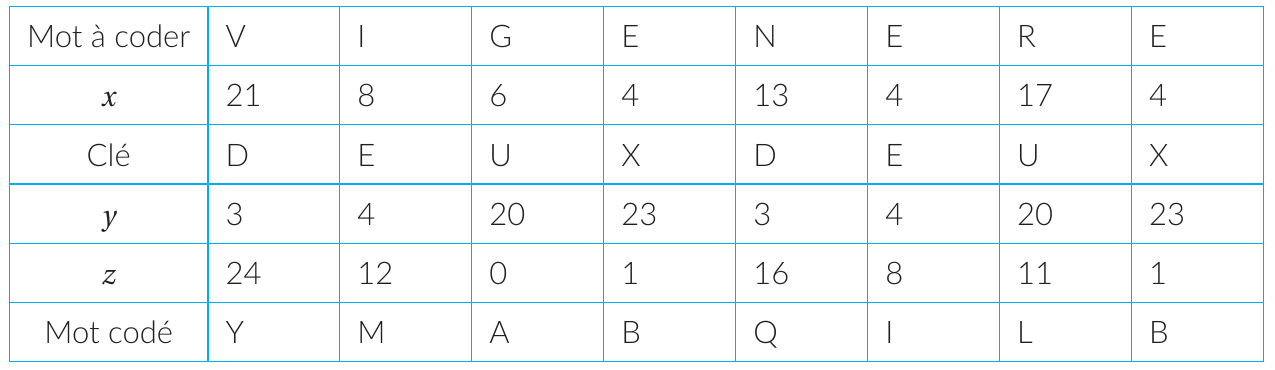
On considère le chiffrement de Vigenère utilisant la clé NSI.
- Par quel mot est codé le mot
RECURSIVITE? - Déchiffrer le mot
CJWTJIZEM.
Le chiffrement AES
Il est actuellement le plus utilisé et le plus sûr est le chiffrement Advanced Encryption Standard ou AES (litt. « norme de chiffrement avancé »), aussi connu sous le nom de Rijndael.
Il devint dans les années 2000, le nouveau standard de chiffrement pour les organisations du gouvernement des États-Unis. Il a été approuvé par la NSA (National Security Agency) dans sa suite B1 des algorithmes cryptographiques.
Il devint dans les années 2000, le nouveau standard de chiffrement pour les organisations du gouvernement des États-Unis. Il a été approuvé par la NSA (National Security Agency) dans sa suite B1 des algorithmes cryptographiques.
Le gouvernement américain a annoncé en juin 2003 à propos de l'algorithme AES (suivant une analyse de la
NSA) :
« L'architecture et la longueur de toutes les tailles de clés de l'algorithme AES (128, 192 et 256) sont suffisantes pour protéger des documents classifiés jusqu'au niveau « SECRET ». Le niveau « TOP SECRET » nécessite des clés de 192 ou 256 bits. L'implémentation de l'AES dans des produits destinés à la protection des systèmes et/ou documents liés à la sécurité nationale doit faire l'objet d'une analyse et d'une certification par la NSA avant leur acquisition et leur utilisation »
« L'architecture et la longueur de toutes les tailles de clés de l'algorithme AES (128, 192 et 256) sont suffisantes pour protéger des documents classifiés jusqu'au niveau « SECRET ». Le niveau « TOP SECRET » nécessite des clés de 192 ou 256 bits. L'implémentation de l'AES dans des produits destinés à la protection des systèmes et/ou documents liés à la sécurité nationale doit faire l'objet d'une analyse et d'une certification par la NSA avant leur acquisition et leur utilisation »
Source : Wikipédia
Nombre de combinaisons à tester pour un chiffrement en 128 bits :
340 282 366 920 938 463 463 374 607 431 768 211 456
340 282 366 920 938 463 463 374 607 431 768 211 456
Chiffrement asymétrique
R.S.A
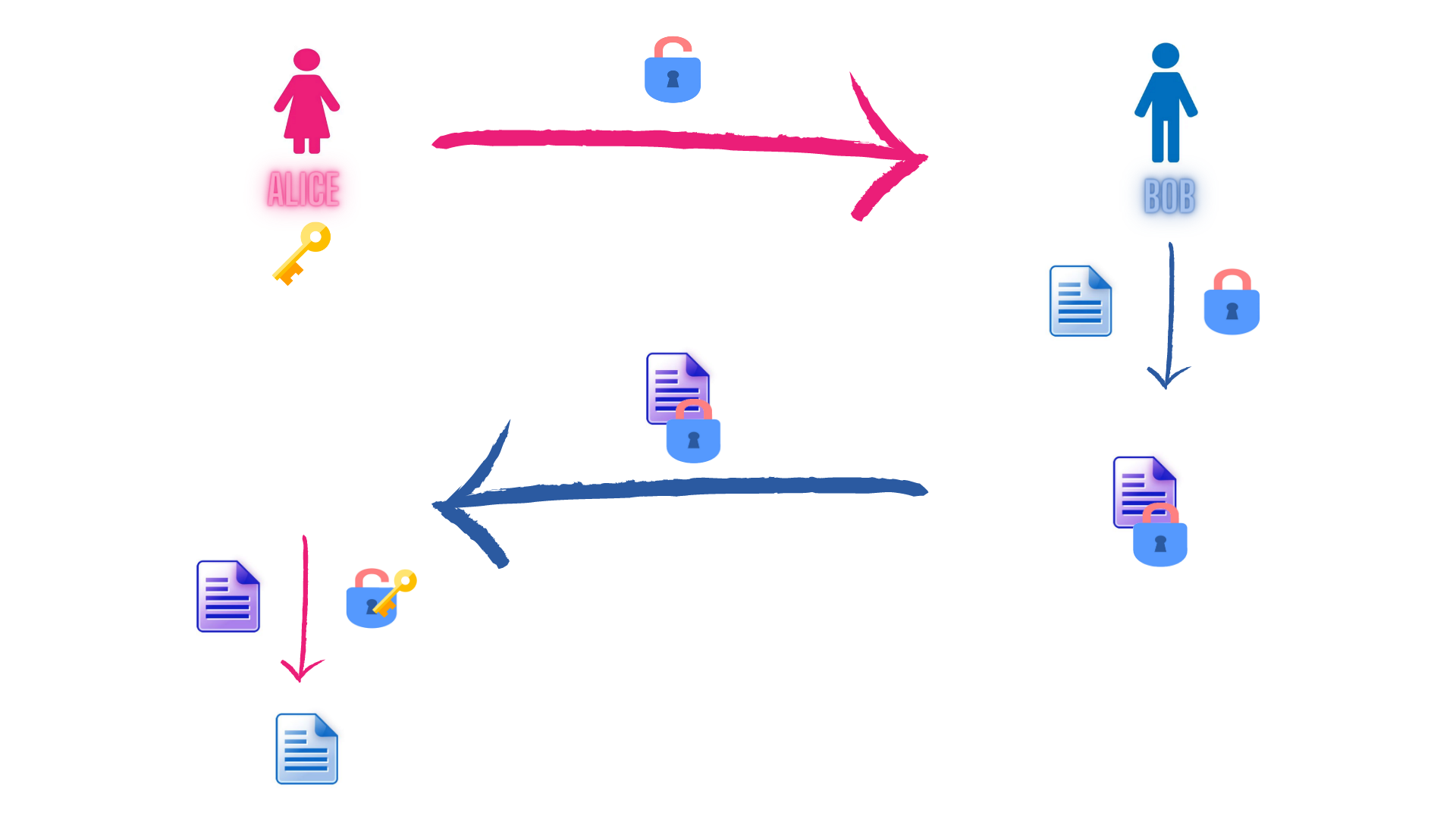
Bob et Alice
Bob veut invité Alice à manger.
Pour cela il doit un message avec l'heure du rendez-vous à Alice mais ne veut pas que Eve puisse le lire.
L'arithmétique modulaire (%)
Soit deux nombres a et b tel que a \leq b
Alors il existe un unique couple (q~;~r) tel que 0 \leq r \lt a et
b = q \times a + r
On dit alors que b \equiv r \mod{a} ( b est congrus à r modulo a)

Nombres premiers entre eux
Soit deux nombres a et b tel que a \lt b.
On dit que a est un diviseur de b quand il existe m tel que b = m \times a
Dans ce cas :
b \equiv 0 \mod{a}
Nombres premiers entre eux
Soit deux nombres a et b. On dit que a et b sont premiers entre eux quand le seul diviseur commun entre ces deux nombres est 1.
Exemple : 9 et 10 sont premiers entre-eux
- Diviseurs de 9 : 1 , 2 , 5 , 10
- Diviseurs de 10 : 1 , 3, 9
Préparation de clé
Alice choisi deux nombres premiers ,p et q, et les multiplie entre eux. Le produit est noté n
p = 13 et q =
11 donc n=146
Elle calcule \phi(n)
\phi(n) = (13 - 1)\times (11 - 1) = 12
\times 10 = 120
On trouve un nombre e premier avec \phi(n)
e = 77
par exemple d(77) = (1,7,11,77)
et d(120) =
(1,2,4,5,6,8,10,12,15,20,24,30,60,120)
Elle déterminer d l’inverse de e modulo \phi(n) un entier relatif.
d = 53 en
effet
53 \times 77 = 4081 = 120 \times 34 +1 donc
4081 \equiv 1 \mod[120]
Préparation de clé :
Clé privée : (53, 143)
Clé public : (77, 143)
Utlisation :
Bob veut envoyer un message (le
nombre 9) à Alice, il demande la clé public d'Alice.
Alice lui envoie le couple (77, 143).
Bob calcule 9^{77} \equiv 81 \mod{143} et envoie le nombre 81 à Alice.
Alice décode le nombre en
calculant 81^{53} \equiv 9 \mod{143}.