Pourquoi les graphes ?
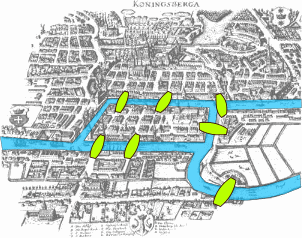
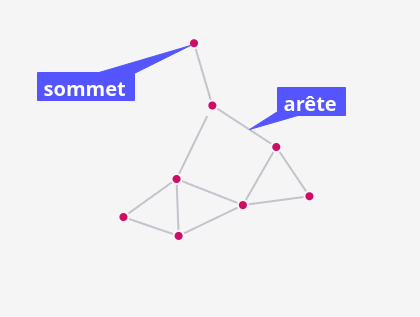
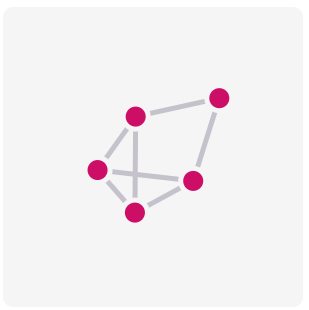
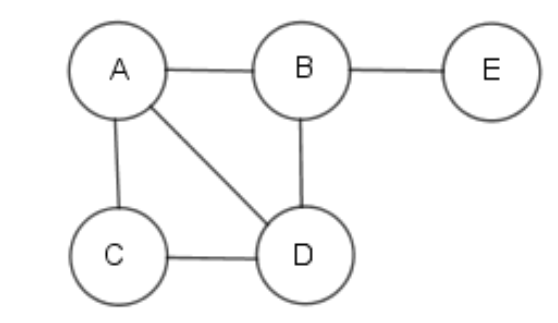
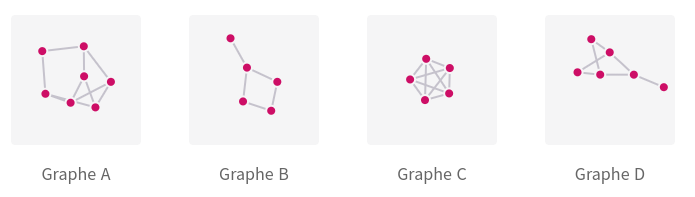
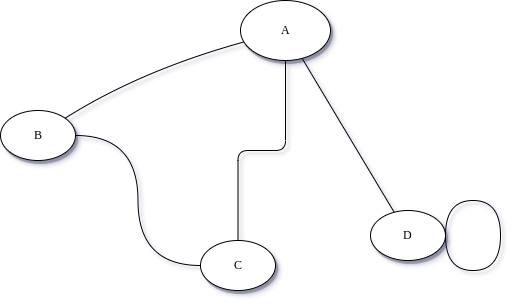
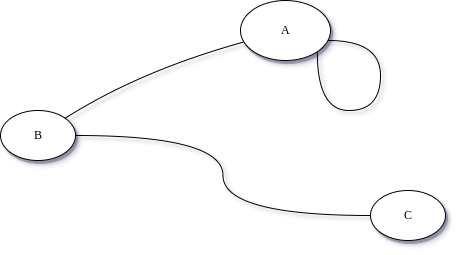
Dans le cours sur les réseaux, nous avions représenté les routeurs par des cercles et les connexions entre eux par des traits.Cette représentation correspond à un graphe.
Il existe de nombreuses autres applications : réseaux informatiques, réseaux urbains, circuits électroniques, liaisons moléculaires, réseaux sociaux...