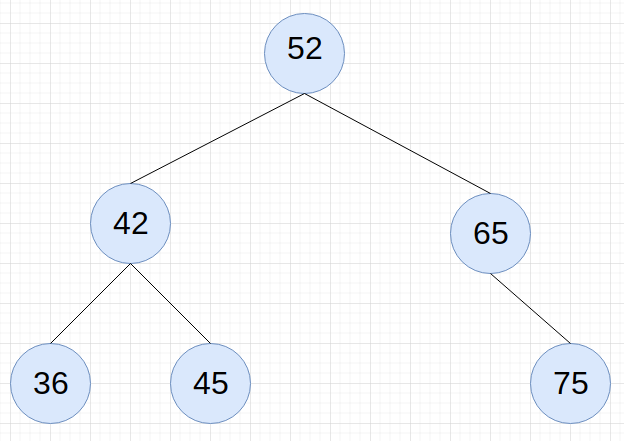
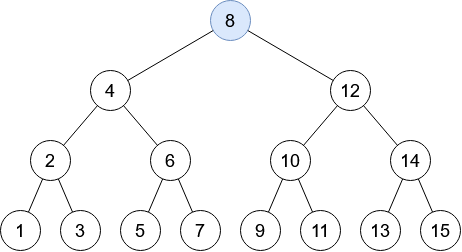
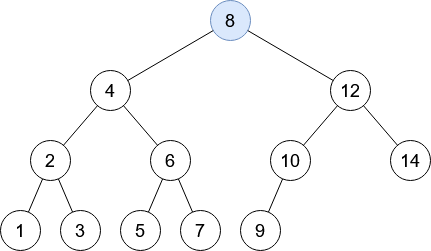
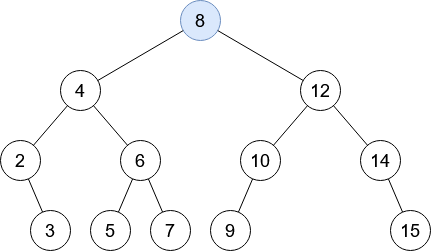
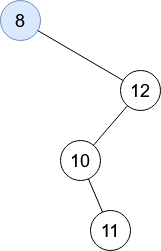
Rechercher le nombre 13 dans cet arbre binaire de recherche
54
26
72
13
48
66
103