Fonctions \cos et \sin
- La fonction cosinus est la fonction définie sur \mathbb{R} qui, à tout réel x, associe \cos(x).
- La fonction sinus, est la fonction définie sur \mathbb{R} qui, à tout réel x, associe \sin(x)
Représentation graphique
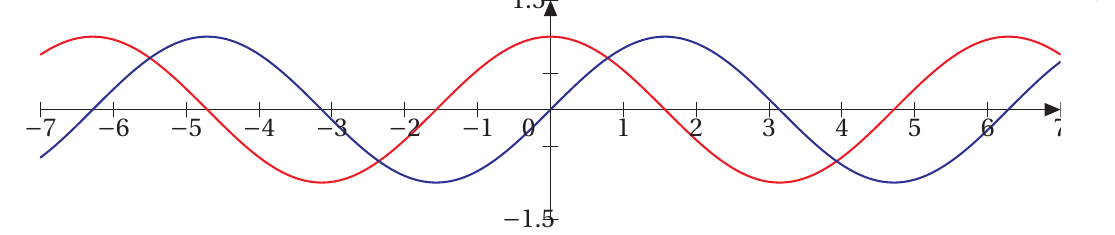
Continuité
- La fonction cosinus est continue sur \mathbb{R}.
- La fonction sinus est continue sur \mathbb{R}.
Parité
- La fonction cosinus est une fonction paire, on a donc \cos(-x) = \cos(x)
- La fonction sinus, est une fonction impaire, on a donc \sin(-x) = \sin(x)
Périodicité
Les fonctions \cos(x) et \sin(x) sont 2\pi-périodique.- \cos(x + 2k\pi) = \cos(x) avec k \in \mathbb{Z}
- \sin(x + 2k\pi) = \sin(x) avec k \in \mathbb{Z}
Dérivée

Tableau de variations : cos
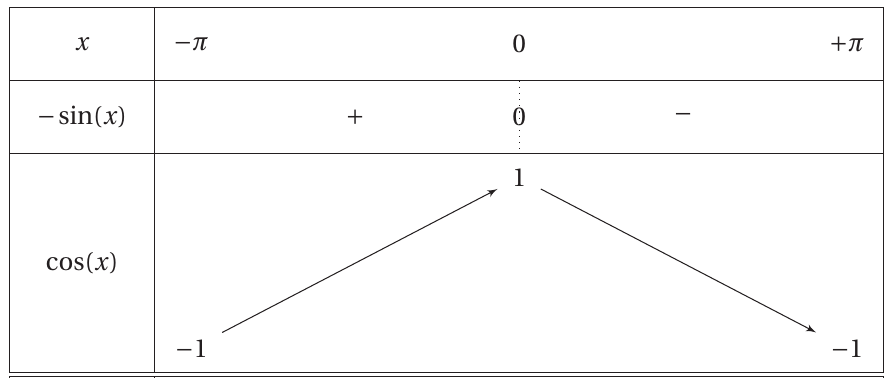
Tableau de variations : sin
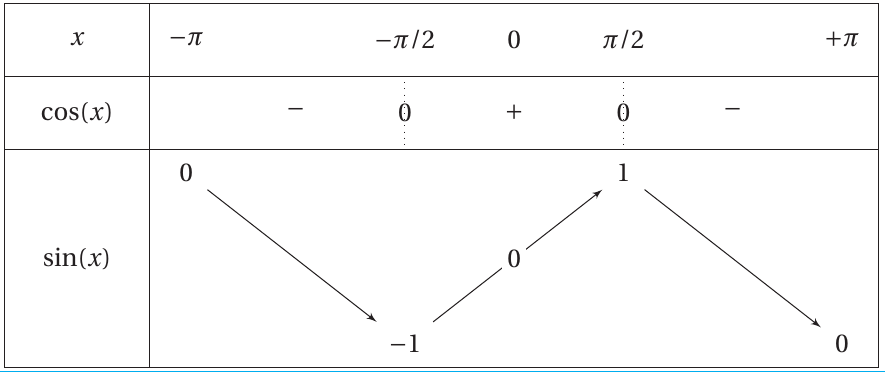
On considère la fonction f, définie sur R par f (x) = \cos(x ) +
\sin( x )
- Donner la valeur exacte de f(-\dfrac{65\pi}{6})
- La fonction f est-elle paire ? impaire ?
- La fonction f est-elle de période 2\pi ? Est-elle de période \pi ?
Soit t la fonction définie sur \mathbb{R}
par
t(x) = 1 + \cos(2x).
- Justifier que t est paire et de période \pi
- Dresser le tableau de variation de t sur l’intervalle 0 ; \dfrac{\pi}{2} ⎣
- En déduire, à l’aide de la question 1, le tableau de variation de t sur l’intervalle [- \pi ; \pi ]



