- A(-1~;~-6.5)
- B(5~;~2.5)
Activité.
Conjecturer le nombres de solutions de l'équation f(x) = 3
Continuité
Chapitre
Théorème des valeurs intermédiaires
Activité.
Conjecturer le nombres de solutions de l'équation f(x) = 3
Activité.
Conjecturer le nombres de solutions de l'équation f(x) = 3
Activité.
Conjecturer le nombres de solutions de l'équation f(x) = 3
Activité.
Conjecturer le nombres de solutions de l'équation f(x) = 3
Activité.
Conjecturer le nombres de solutions de l'équation f(x) = 3
Découverte
Toutes les fonctions utilisées dans cette partie sont définies sur l'intervalle [-1~;~5] et passe par les points :
Solution de l'équation f(x) = 1
Solution de l'équation g(x) = 1
Solution de l'équation i(x) = 1
Théorème des valeurs intermédiaires
Soit f une fonction définie et continue sur un intervalle [a~;~b].Pour tout réel k compris entre f (a) et f (b) , il existe au moins un réel c compris entre a et b tel que f (c) = k .
Conséquence
Dans ces conditions, l'équation f(x) = c admet au moins une solution dans l'intervalle [a~;~b].Corollaire
Nombre de solutions de l'équation f(x) = -1
Nombre de solutions de l'équation g(x) = -1
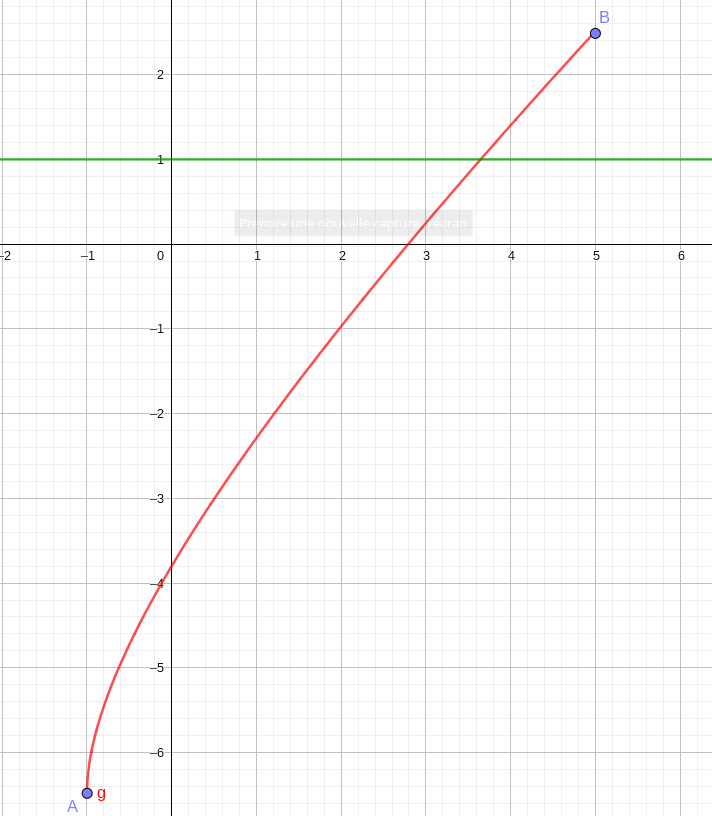
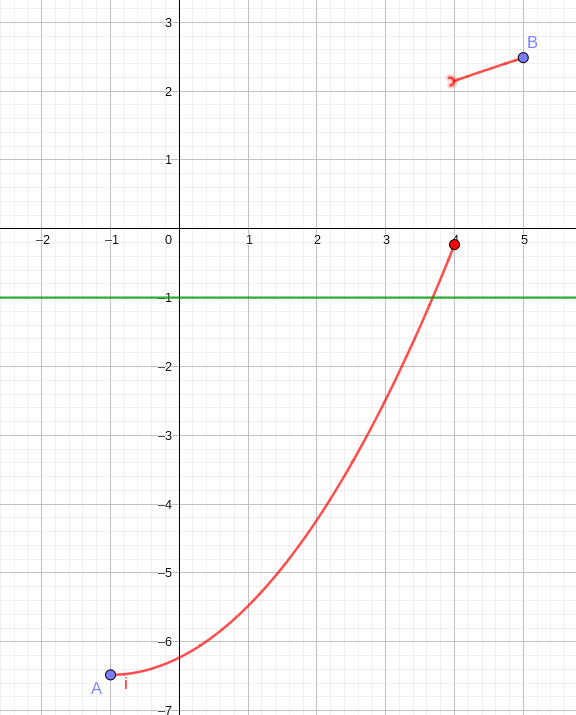
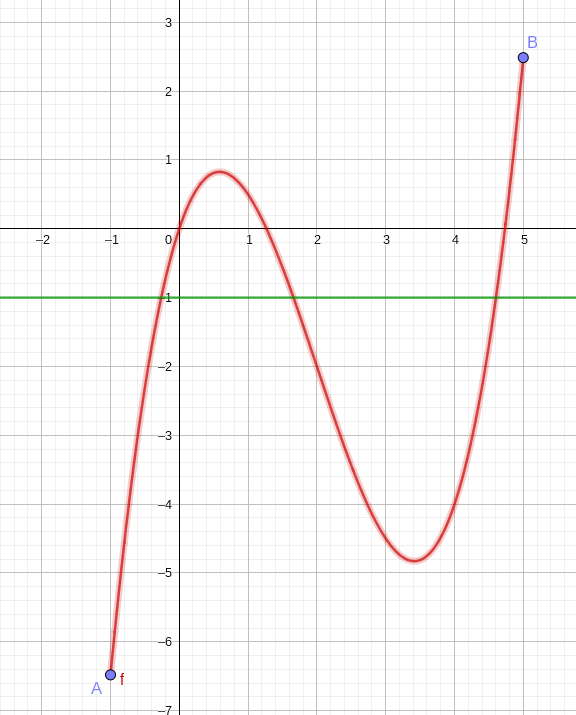
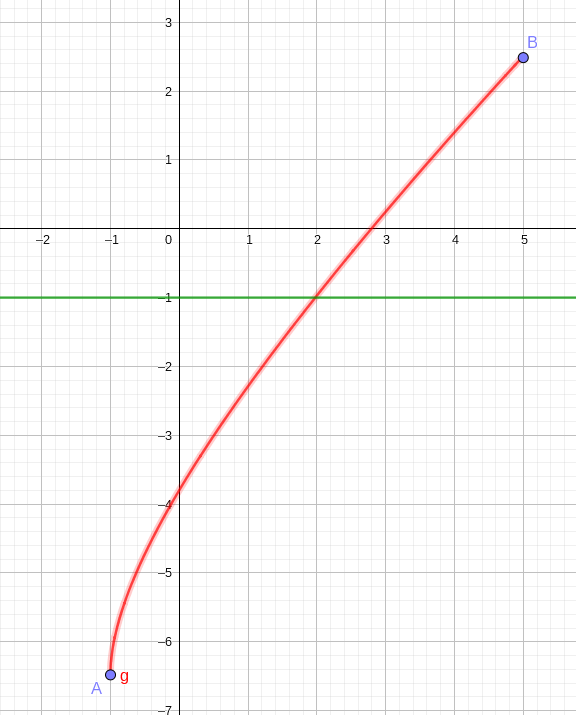
Corollaire
Soit f une fonction définie continue et strictement croissante( resp. strictement décroissante ) sur un intervalle [a~;~b].Pour tout réel k \in [f(a)~;~f (b)] (resp. k \in [f(b)~;~f (a)] ) , il existe un unique réel c \in [a~;b] tel que f (c) = k .
36 p. 133
36 p. 133
65 p. 136
Type BAC
Type BAC
