Objectifs
- Montrer que la suite associé à une suite arithmético-geométrique est une suite géométrique;
- Déterminer la forme explicite d'une suite arithmético-geométrique à partir de sa suite associée.
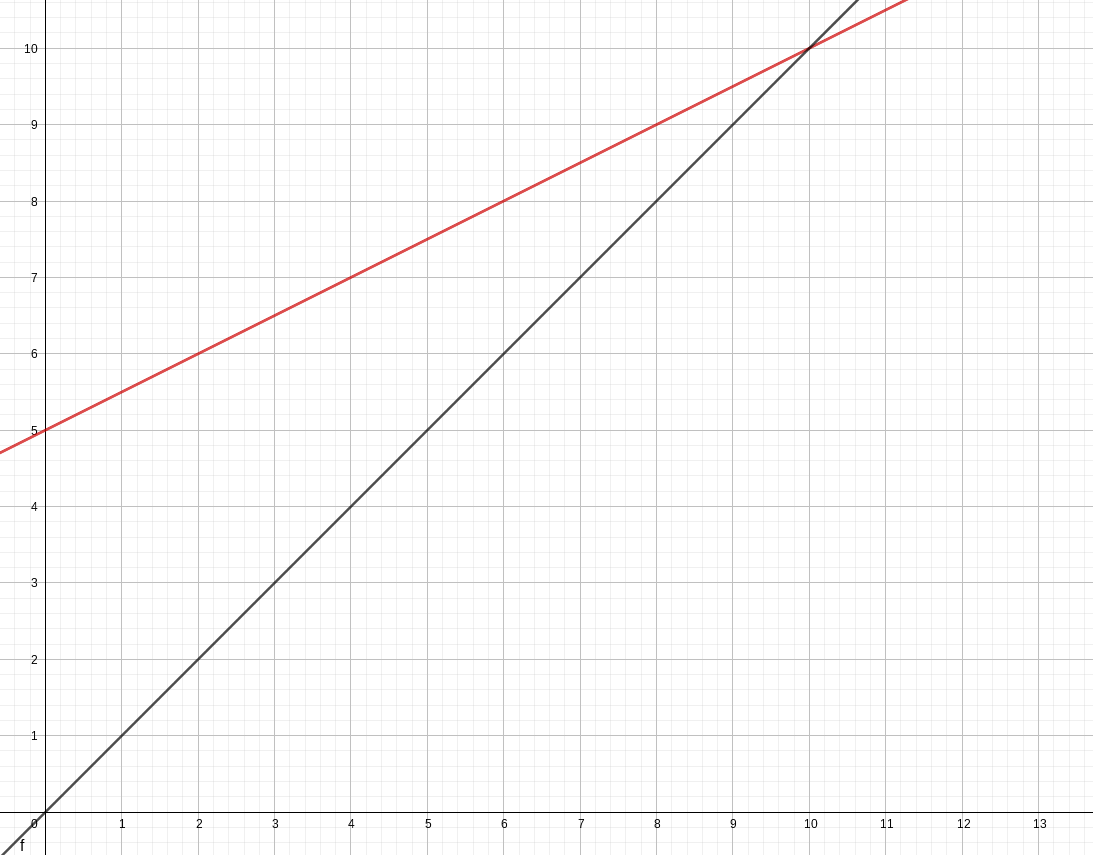
point fixe de la fonction
affine f définie par f(x) = ax + b, c’est-à-dire f(\alpha) = \alpha.