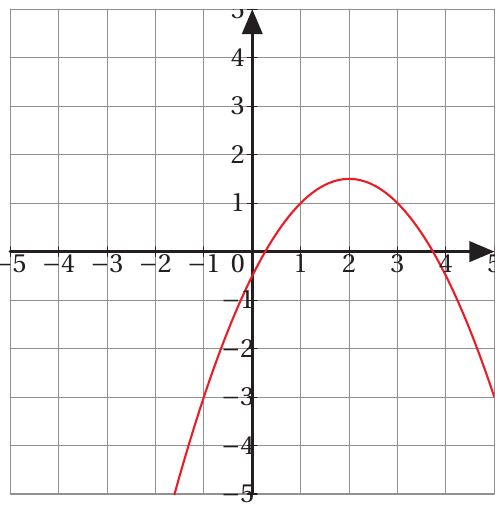
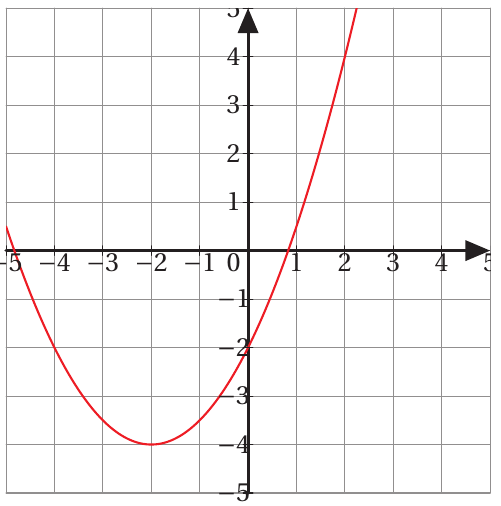
P(x) = ax^2 + bx +c
P(x) = a\left(x^2 + \dfrac{b}{a}x\right) +c
P(x) = a\left(x^2 + 2\dfrac{b}{2a}x + \dfrac{b^2}{4a^2} - \dfrac{b^2}{4a^2} \right) +c
P(x) = a\left(x^2 + 2\dfrac{b}{2a}x + \dfrac{b^2}{4a^2}\right) - a\dfrac{b^2}{4a^2} +c
P(x) = a\left(x^2 + 2\dfrac{b}{2a}x + \dfrac{b^2}{4a^2}\right) - \dfrac{b^2}{4a} + c
P(x) = a\left(x^2 + \dfrac{b}{2a}\right)^2 - \dfrac{b^2}{4a} + c
P(x) = a\left(x^2 + \dfrac{b}{2a}\right)^2 - \dfrac{b^2 - 4ac}{4a}
En posant :
\alpha = -\dfrac{b}{2a} \beta = -\dfrac{b^2 - 4ac}{4a}
La forme canonique d'un polynôme du second degré est l'écriture du polynôme sous la forme :
P(x) = a(x - \alpha)^2 + \beta