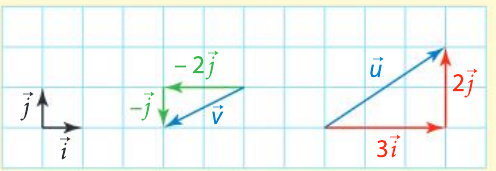
Propriété
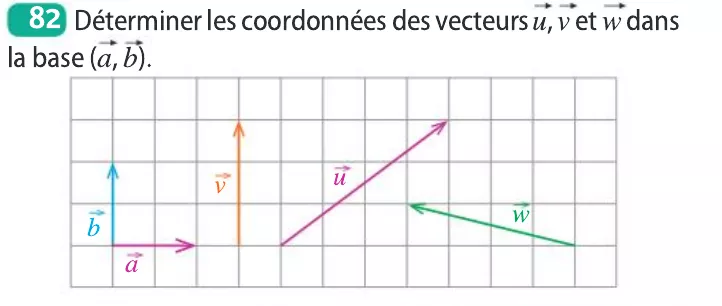
Soit (\overrightarrow{i} , \overrightarrow{j} ) une base du plan.
Pour tout vecteur \overrightarrow{u}, il existe un unique couple de nombres ( x~;~y ) tels que \overrightarrow{u} = x\overrightarrow{i} + y\overrightarrow{j} .
On dit que \overrightarrow{u} a pour coordonnées (x~;~y) dans cette base.
On le note \overrightarrow{u} \left( \begin{array}{c} x \\ y \end{array} \right)
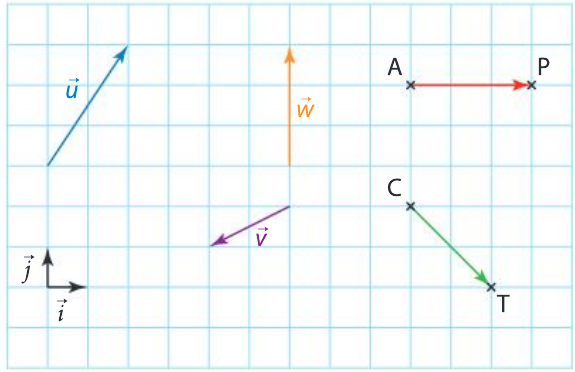
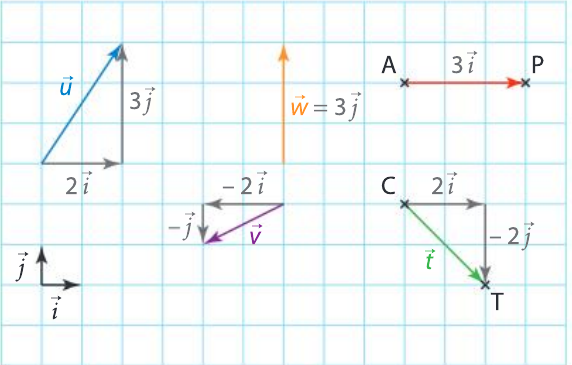
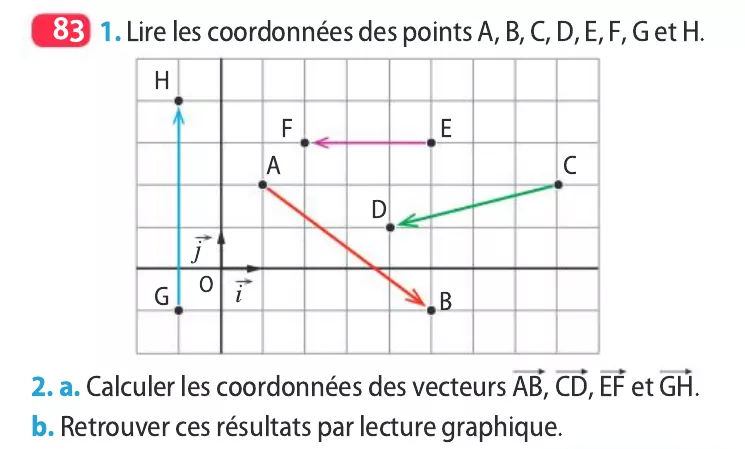
Déterminer les coordonnées de
\overrightarrow{u} \text{ et } \overrightarrow{v} dans la base
(O ; \overrightarrow{i} , \overrightarrow{j} )
Opérations sur les coordonnées
Soit une base orthonormée
\left( \vec{i}, \vec{j}\right) du plan, et
k un nombre réel.
Si
\vec{u} \left( \begin{array}{c} x \\ y\end{array} \right) et
\vec{v} \left( \begin{array}{c} x' \\ y' \end{array} \right), alors :
- \vec{u} + \vec{v} = \left( \begin{array}{c} x+x' \\ y + y' \end{array} \right)
- \vec{u} - \vec{v} = \left( \begin{array}{c} x -x' \\ y - y' \end{array} \right)
- k\vec{u} = \left( \begin{array}{c} kx \\ ky \end{array} \right)
Repère orthonormé
- Un repère orthonormé (O ; \overrightarrow{i} , \overrightarrow{j} ) est formé d’un point O et de deux vecteurs \overrightarrow{i} \text{ et } \overrightarrow{j} ) du plan de même norme et de direction perpendiculaire.
- Pour tout point M du plan, le couple de coordonnées de M dans le repère (O ; \overrightarrow{i} , \overrightarrow{j} ) est le couple (x, y) tel que : \overrightarrow{OM} = x\overrightarrow{i} + y\overrightarrow{j} ou encore \overrightarrow{OM} \left( \begin{array}{c} x \\ y \end{array} \right)
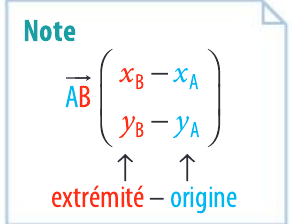
Coordonnées d'un vecteur
Pour tout points
A(x_A~;~y_A) et
B(x_B~;~y_B) dans un repère
(O ; \overrightarrow{i} , \overrightarrow{j} ), le vecteur
\overrightarrow{AB} a pour coordonnées
\overrightarrow{AB} \left( \begin{array}{c} x_B - x_A \\ y_B - y_A \end{array} \right)
Egalité de 2 vecteurs
Soit une base et les vecteurs \overrightarrow{u} \left( \begin{array}{c} x \\ y \end{array} \right) et \overrightarrow{v} \left( \begin{array}{c} x' \\ y' \end{array} \right) .
Alors \overrightarrow{u} = \overrightarrow{v} si et seulement si x= x' et y = y'
Milieu d'un segment
I est le milieu de [AB], si et seulement si
\overrightarrow{AI} = \overrightarrow{IB}
Coordonnées du milieu d'un segment
Pour tout points A(x_A~;~y_A) et B(x_B~;~y_B) dans un repère (O ; \overrightarrow{i} , \overrightarrow{j} ), le milieu I de [AB] a pour coordonnées \left( \dfrac{x_A + x_B}{2}~;~ \dfrac{y_A + y_B}{2}\right)