Infographie
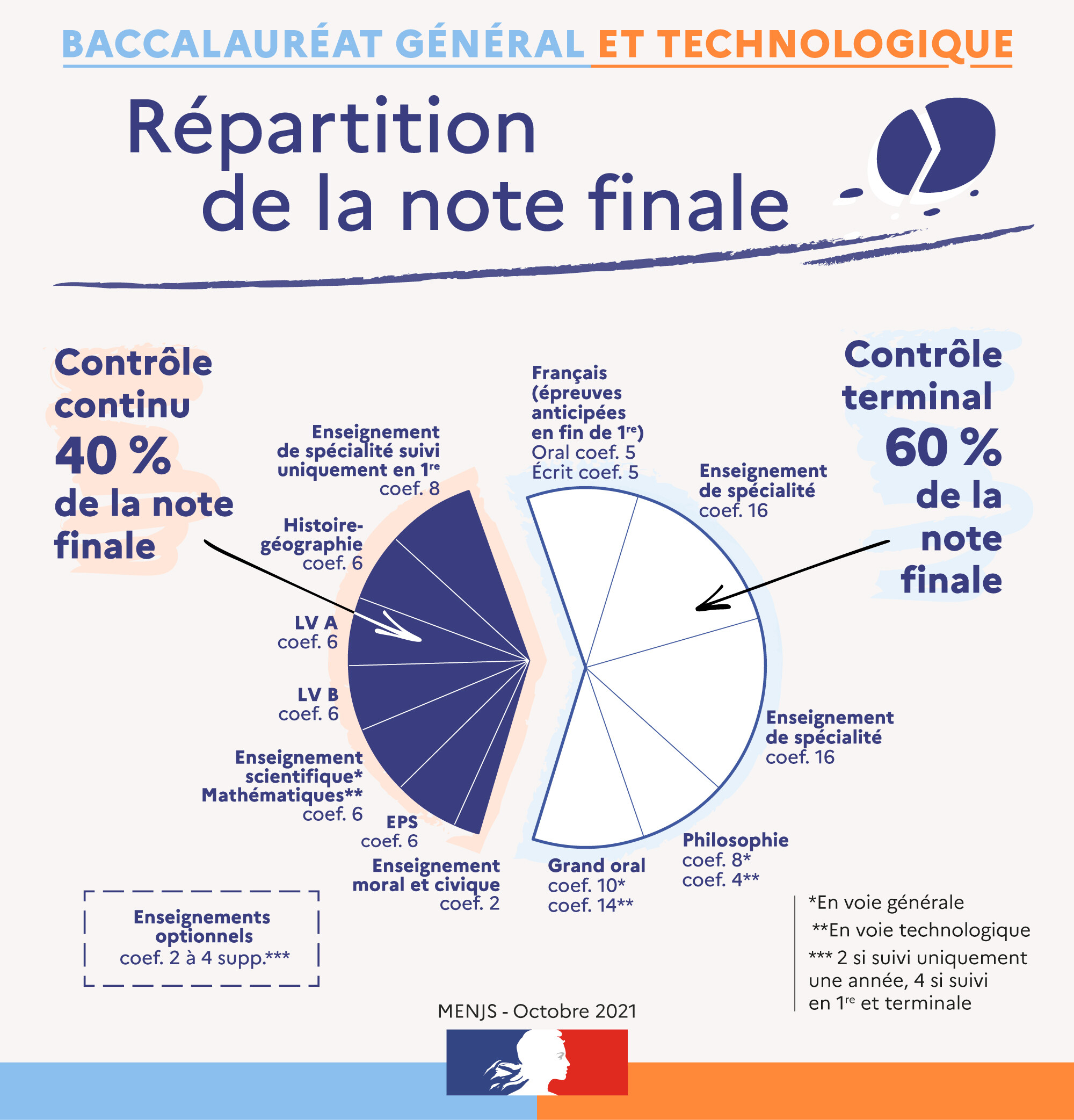

| Matières | Français Oral | Français Ecrit | Spé 1ère | Hist. Géo. | LV A | LV B | Ens. Sci. | E.P.S |
|---|---|---|---|---|---|---|---|---|
| Coefficient | 5 | 5 | 8 | 6 | 6 | 6 | 6 | 6 |
| Notes | 10 | 8 | 12 | 13 | 14 | 12 | 6 | 16 |
| Matières | E.M.C | Spe 1 | Spe 2 | Philosophie | Grand Oral |
|---|---|---|---|---|---|
| Coefficient | 2 | 16 | 16 | 8 | 10 |
| Notes | 12 | 9 | 13 | 15 | 9 |
| Nombre de buts x_i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Nombre de match n_i | 7 | 17 | 13 | 14 | 8 | 6 | 0 | 1 |
L’effectif cumulé croissant (noté E.C.C.) d’une valeur est égal à la somme de l’effectif de cette valeur plus les effectifs des valeurs qui lui sont inférieures.
Compléter le tableau ci-dessous.
| Salaire | 1500 | 1600 | 1800 | 2000 | 2300 | 2500 |
|---|---|---|---|---|---|---|
| Effectif | 25 | 34 | 51 | 31 | 24 | 12 |
| E.C.C. |
Le tableau ci-dessous donne le nombre de but marqués par match durant un tournoi de football.
| Nombre de buts | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Nombre de matchs | 3 | 4 | 7 | 9 | 6 | 3 | 4 | 1 | 3 |
| E.C.C. |
On a relevé, dans un jeu télévisé, le nombre de candidats ayant répondu correctement à une liste de questions.
| Nombre de réponses | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Effectifs | 1 | 2 | 5 | 8 | 15 | 45 | 32 | 21 | 9 | 2 |
| E.C.C. |