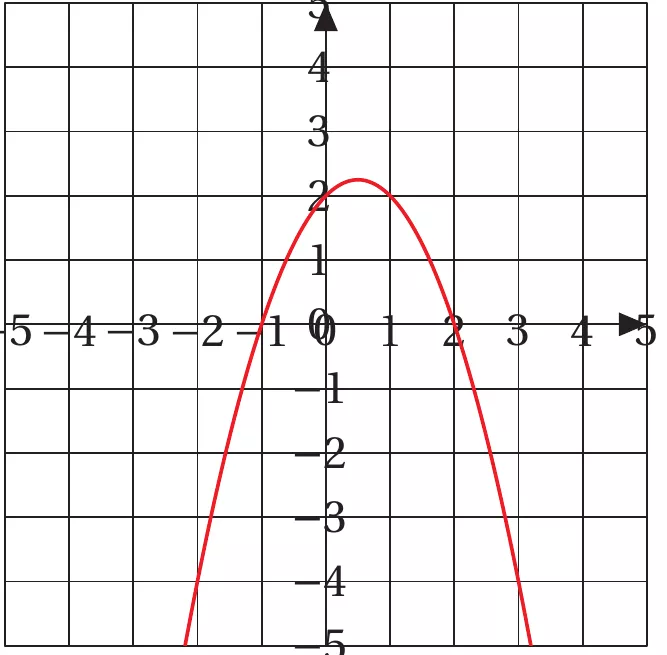
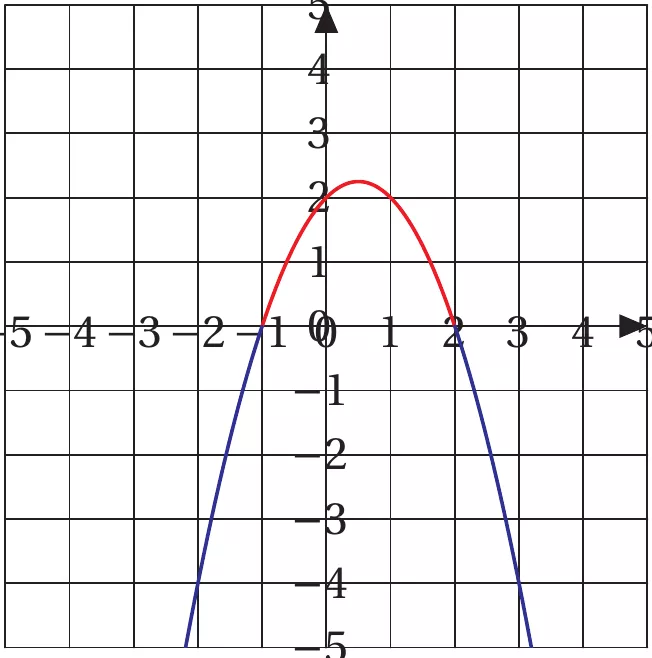
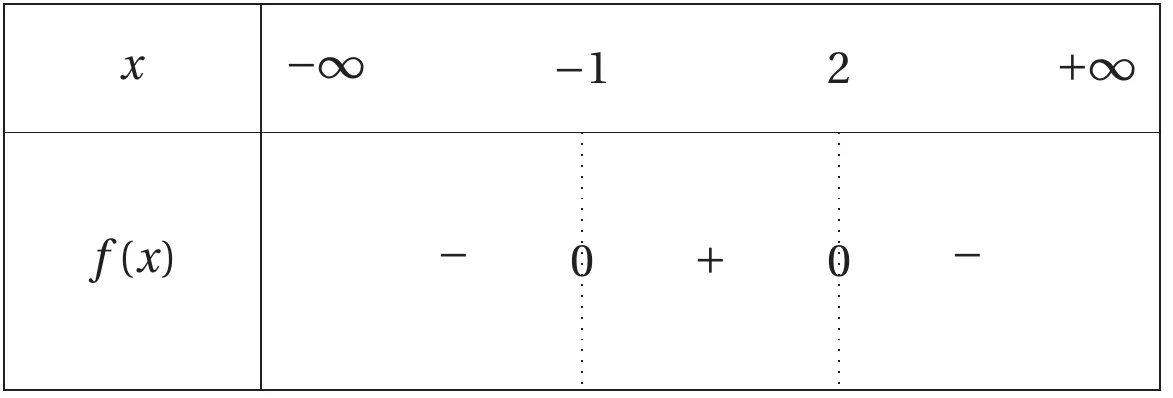
Exemple
Soit f une fonction définie par les associations suivantes :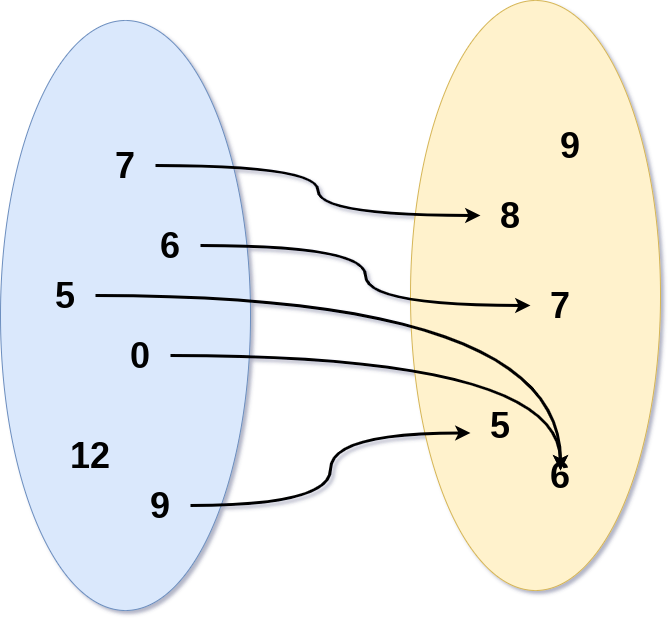
- Quelle est l'image de 5 par la fonction f ?
- Déterminer f(7) .
- Déterminer un antécédent de 6.
- Déterminer un antécédent de 9.
Une fonction est un processus qui associe à chaque nombre un unique nombre appelé image.
Dans l'activité sur le marnage, on associait l'heure à la hauteur de la marée.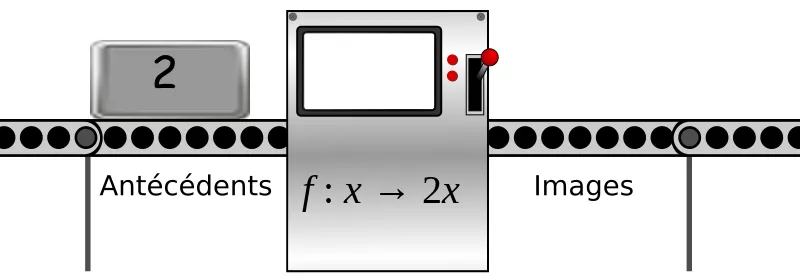
antécédent de
f(x) par f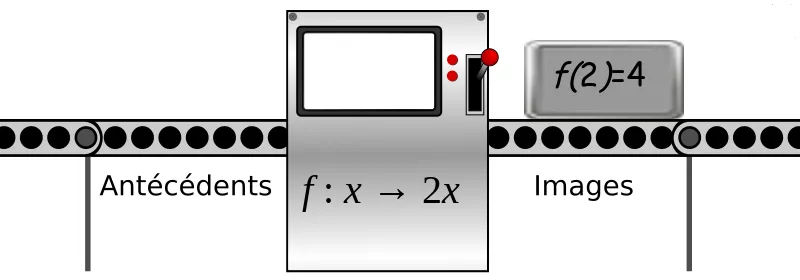
antécédent de
f(x) par fl'image de

(x;f(x)). 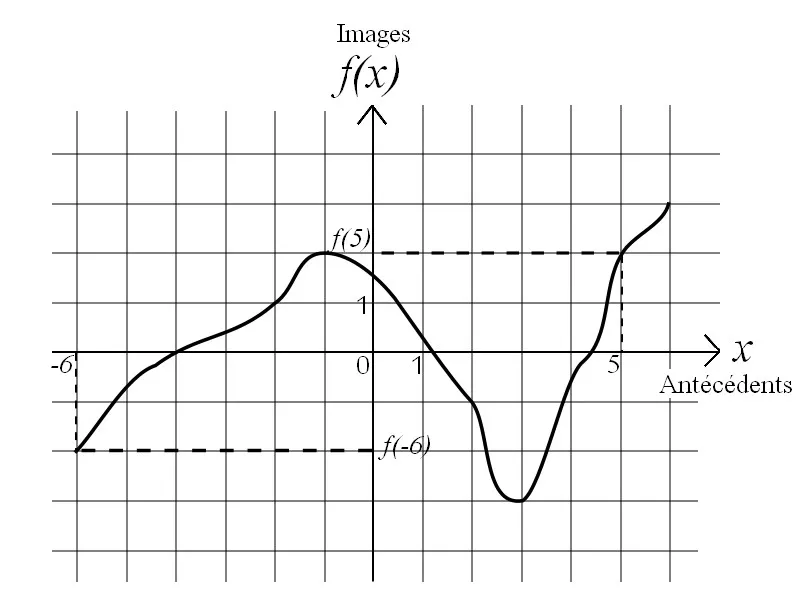
 Quizz
Quizz