Chapitre 2
Ensemble de nombres
Ensembles de nombre.
Classer par groupe les nombres ci-dessous :
\pi
-\dfrac{12}{3}
0
-5 \times 10^{-3}
\dfrac{3}{7}
-\dfrac{12}{3}
0
-5 \times 10^{-3}
\dfrac{3}{7}
-42
\dfrac{7}{5}
\sqrt{2}
\dfrac{1}{3}
\dfrac{15}{5}
\dfrac{7}{5}
\sqrt{2}
\dfrac{1}{3}
\dfrac{15}{5}
-\sqrt{0,64}
-\sqrt{9}
-4,07
\sqrt{36}
\dfrac{3}{2}
-\sqrt{9}
-4,07
\sqrt{36}
\dfrac{3}{2}
0,142857~142857~...
2,6 \times 10 ^2
-3,3 \times 10^1
\dfrac{2}{3}
\sqrt{\dfrac{49}{81}}
2,6 \times 10 ^2
-3,3 \times 10^1
\dfrac{2}{3}
\sqrt{\dfrac{49}{81}}
définitions
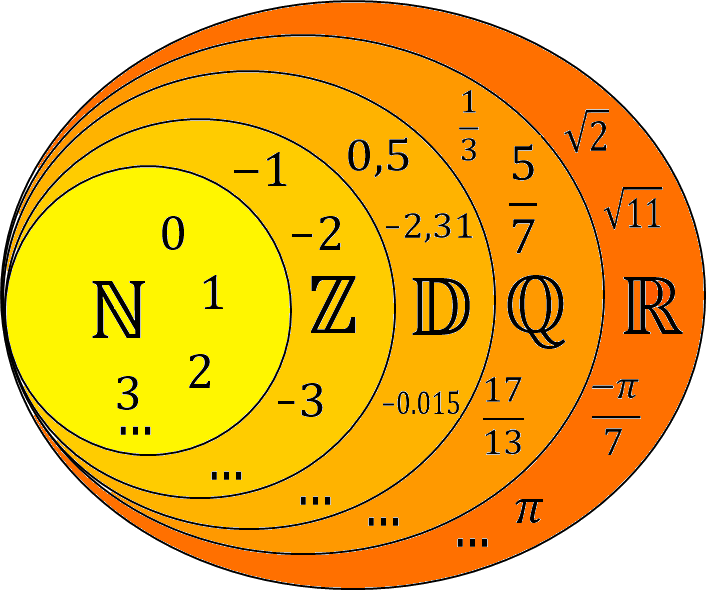
L'ensemble \mathbb{N}
L'ensemble des entiers naturels, noté \mathbb{N} est l'ensemble des nombres entiers positifs : 0, 1, 2, ...L'ensemble \mathbb{Z}
L'ensemble des entiers relatifs, noté \mathbb{Z}, est l'ensemble des nombres naturels et de leurs opposées : ..., -2, -1, 0, 1, 2, ...définitions
L'ensemble \mathbb{D}
L'ensemble des nombres décimaux, noté \mathbb{D}, est l'ensemble des nombres qui peuvent s'écrire sous la forme d'une fraction décimale, c'est à dire de la forme \dfrac{p}{10^n} avec p appartenant à \mathbb{Z}.L'ensemble \mathbb{Q}
L'ensemble des nombres rationnels, noté \mathbb{Q}, est l'ensemble des nombres qui peuvent s'écrire sous la forme d'une fraction, c'est à dire de la forme \dfrac{p}{q} avec p appartenant à \mathbb{Z} et q appartenant à \mathbb{N}^*.définition
L'ensemble \mathbb{R}
L'ensemble des nombres réels, noté \mathbb{R}, est l'ensemble des nombres exprimant une longueur ou l'opposé d'un nombre représentant une longueur.
définition
Les notations \in et \notin
- Quand un nombre n appartient à un ensemble \mathbb{E}, on le note
n \in \mathbb{E} - Quand un nombre n n'appartient pas à un ensemble \mathbb{E}, on le note \notin:
n \notin \mathbb{E}
\pi
-\dfrac{12}{3}
0
-5 \times 10^{-3}
\dfrac{3}{7}
-\dfrac{12}{3}
0
-5 \times 10^{-3}
\dfrac{3}{7}
-42
\dfrac{7}{5}
\sqrt{2}
\dfrac{1}{3}
\dfrac{15}{5}
\dfrac{7}{5}
\sqrt{2}
\dfrac{1}{3}
\dfrac{15}{5}
-\sqrt{0,64}
-\sqrt{9}
-4,07
\sqrt{36}
\dfrac{3}{2}
-\sqrt{9}
-4,07
\sqrt{36}
\dfrac{3}{2}
0,142857~142857~...
2,6 \times 10 ^2
-3,3 \times 10^1
\dfrac{2}{3}
\sqrt{\dfrac{49}{81}}
2,6 \times 10 ^2
-3,3 \times 10^1
\dfrac{2}{3}
\sqrt{\dfrac{49}{81}}
| \mathbb{N} | \mathbb{Z} | \mathbb{D} | \mathbb{Q} | \mathbb{R} | |
| \pi | |||||
| -\frac{12}{3} | |||||
| 0 | |||||
| -5 \times 10^{-3} | |||||
| \frac{3}{7} | |||||
| -42 | |||||
| \frac{7}{5} | |||||
| \sqrt{2} | |||||
| \frac{1}{3} | |||||
| \frac{15}{5} |
| \mathbb{N} | \mathbb{Z} | \mathbb{D} | \mathbb{Q} | \mathbb{R} | |
| -\sqrt{0,64} | |||||
| -\sqrt{9} | |||||
| -4,07 | |||||
| \sqrt{36} | |||||
| \frac{3}{2} | |||||
| 0,142857~142857~... | |||||
| 2,6 \times 10 ^2 | |||||
| -3,3 \times 10^1 | |||||
| \frac{2}{3} | |||||
| \sqrt{\frac{49}{81}} |
Nombre entier et relatifs
Multiple, diviseur et nombres pairs
Multiples et diviseurs
Soit a et b deux entiers.On dit que a est un multiple de b s'il existe un entier k tel que a = k \times b.
Dans ce cas là, on dit aussi que b est un diviseur de a.
12 est divisible par 3
On dira que :
- 12 est un multiple de 3
- 3 est un diviseur de 12
10 n'est pas divisible par 4
Ensemble des diviseurs
Notons tous les diviseurs de 60
60 = 1 × 60 = 2 × 30 = 3 × 20 = 4 × 15 = 5 × 12 = 6 × 10.
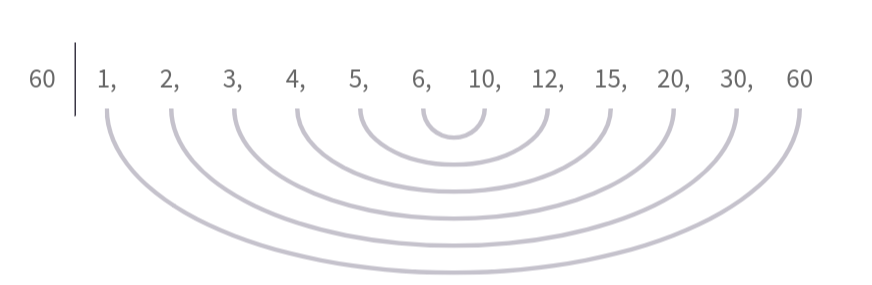
L'ensemble des diviseurs de 60 est donc : {1,2,3,4,5,6,10,12,15,20,30,60}
Pour trouver tous les facteurs d’un nombre, nous commençons simplement aux deux extrémités de cette liste,
jusqu’à ce qu'on se trouver au milieu.
Exercice 17 p.64
Exercice 22 p.64
Exercice 27 p.65
Exercice 48 p.66
Exercice 56 p.66
Exercice 63 p.66
Exercice 64 p.66
Pairs et impairs
- Un nombre pair est un entier multiple de 2.
On peut l'écrire sous la forme 2k avec k entier. -
Un nombre impair est un entier non multpiple de 2.
On peut l'écrire sous la forme 2k+1 avec k entier.
Exercice 28 p.65
Démontrer que le carré d'un nombre impair est impair.
Nombres premiers & Nombres composés
On dit d'un nombre entier qu'il est premier lorsqu'il admet uniquement deux diviseurs distincts : 1 et lui-même.Exemple
La suite des nombres premiers débutent par 2, 3, 5, 7, 11, 13, 17, 19...On remarque que 1 n'est pas premier.
A contrario, 6 = 3 \times 2, ou encore 15 = 3 \times 5 ne sont pas des nombres premiers.
Nombres composés
Par opposition, un nombre entier qui n'est pas premier est dit composé.Exemple
6 et 15 sont des nombres composés.Exercice 30 p.65
Exercice 32 p.65
Exercice 33 p.65
Exercice 94 p.68
Exercice 62 p.66
Les nombres rationnels
Démonstration par l'absurde
Démontrer par l'absurde qu'un nombre n'appartient pas à \mathbb{D}Exercice
Montrer que \dfrac{1}{3} \notin \mathbb{D}
Raisonnons par l'absurde :
Supposons que \dfrac{1}{3} in \mathbb{D}
Supposons que \dfrac{1}{3} in \mathbb{D}
Raisonnons par l'absurde :
Supposons que \dfrac{1}{3} = \dfrac{p}{10k}
Supposons que \dfrac{10^k}{3} = p
Supposons que 10^k = 3p
Donc 10^k est divisible par 3 ce qui est impossible car la somme de ces chiffres est 1 .
Supposons que \dfrac{1}{3} = \dfrac{p}{10k}
Supposons que \dfrac{10^k}{3} = p
Supposons que 10^k = 3p
Donc 10^k est divisible par 3 ce qui est impossible car la somme de ces chiffres est 1 .
Démontrer que :
Un nombre est divisible par 7 si et seulement si la somme de son nombre de dizaines et de cinq fois son chiffre des unités l'est.
\dfrac{1}{7} \notin \mathbb{D}
Aide Un nombre est divisible par 7 si et seulement si la somme de son nombre de dizaines et de cinq fois son chiffre des unités l'est.
Opérations sur les nombres rationnels
Fraction irréductible
Une fraction est irréductible lorsque son numérateur et son dénominateur n'ont aucun diviseur commun (autre
que 1).
Il n'est plus possible de la simplifier
Fraction irréductible
Sans l'aide de la calculatrice, déterminer les fractions irreductibles égales à :- \dfrac{36}{24}
- \dfrac{12}{35}
- \dfrac{21}{91}
Sans calculatrice, écrire les expressions suivantes sous forme simplifiée.
- \dfrac{2}{3} + \dfrac{7}{15}
- \dfrac{13}{30}-\dfrac{7}{15} + \dfrac{5}{3}
- \dfrac{-2}{9}-\dfrac{-8}{15}
- \dfrac{2}{11}+2
Sans calculatrice, écrire les expressions suivantes sous forme simplifiée.
- \dfrac{-2}{9}\times\dfrac{-3}{5}
- \dfrac{7}{12}-\dfrac{4}{12} \times \dfrac{3}{5}
- \dfrac{\dfrac{-2}{9}}{\dfrac{-8}{15}}
- \left(\dfrac{2}{11}\right)^2 \div \dfrac{242}{3}
Sans calculatrice, écrire les expressions suivantes sous forme simplifiée.
- \dfrac{2}{3}\left(2+\dfrac{3}{4}\right)
- \dfrac{2}{3}\times 2 + \dfrac{3}{4}
- \dfrac{1}{2} + \dfrac{1}{3}-\dfrac{1}{6}
- \dfrac{1}{2} \div \dfrac{1}{3}\div \dfrac{1}{4}\div \dfrac{1}{5}
Pour aller plus loin ...
Sans calculatrice, détermine l'écriture simplifiée de l'expression :
1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \dfrac{1}{5} + \dfrac{1}{6} + \dfrac{1}{7}
Montrer que pour tout n \in \mathbb{N} tel que n \neq 0
:
\dfrac{1}{n+1} + \dfrac{1}{n} = \dfrac{-1}{n(n+1)}
Soit a,b,c et d quatre nombres réels non nul tel que ad + bc \neq 0.
Montrer que :
Montrer que :
\left(\dfrac{a}{b} + \dfrac{c}{d}\right) \times \dfrac{bd}{ad + bc} = 1
Nombres réels
Intervalles
On appelle un intervalle l'ensemble des nombres réels compris entre deux nombres réels a et b,
ou de manière équivalente l'ensemble des points sur la droite dont la marque est entre a et b.
Exemple : l'intervalle [ 2 ; 5 ] est l'ensemble des nombres réels x tels que 2 ≤ x, et x ≤ 5.
Ouvert & fermé
On dit qu'un intervalle est fermé si ses extrémités appartiennent à l'intervalle.
On dit qu’il est ouvert dans le cas contraire.
Exemple : L’intervalle [– 2 ; 5] est un intervalle fermé.
On a : -2 ∈ [– 2 ; 5] et 5 ∈ [– 2 ; 5]
• L’intervalle ]2 ; 6[ est un intervalle ouvert.
On a : 2 ∉ ]2 ; 6[ et 6 ∉ ]2 ; 6[
Infini
Certains intervalles n'ont qu'une borne.
Exemple : L'ensemble des nombres supérieur ou égal à 3
x \geq 3
x \in ..........
Exercice 2
Exercice 3
Exercice 4
Intersection et union
- L'intersection de deux ensembles A et B est l'ensemble des éléments qui appartiennent à A
et à B et se note A∩B.
- La réunion de deux ensembles A et B est l'ensemble des éléments qui appartiennent à A
ou à B et se note A∪B.
Exemple : L'ensemble des nombres supérieur ou égal à 3
x \geq 3
x \geq 3
Dans les cas suivants, déterminer l'intersection et la réunion des intervalles I et J :
- a) I = [-1 ; 3] et J = ]0 ; 4[
- b) I = ] - ∞ ; -1] et J = [1 ; 4]