Overflow
Tout tenait à une seule petite variable : celle allouée à l'accélération horizontale. En effet, l'accélération horizontale maximum d'Ariane 4 donnait une valeur décimale d'environ 64. Cette valeur étant traitée dans un registre mémoire à 8 bits, cela donne en base binaire 2^8 = 256 valeurs disponibles, un nombre suffisant pour 64.
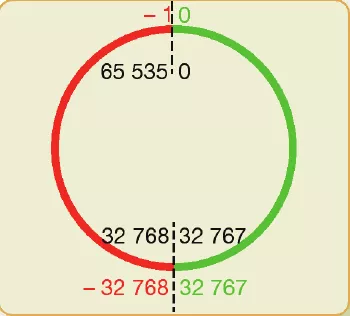
Mais Ariane 5 était bien plus puissante et brutale : son accélération pouvait atteindre la valeur 300, qui donne 100101100_{\overline{2}} et nécessite un registre à 9 bits. Ainsi, la variable codée sur 8 bits a connu un dépassement de capacité, puisque son emplacement mémoire n'était pas assez grand pour accepter une valeur aussi importante. Il aurait fallu la coder sur un bit de plus, donc 9 bits, ce qui aurait permis de stocker une valeur limite de 2^9-1 = 511, alors suffisante pour coder la valeur 300.
De ce dépassement de capacité a résulté une valeur absurde dans la variable, ne correspondant pas à la réalité.
Par effet domino, le logiciel décida de l'autodestruction de la fusée à partir de cette donnée erronée.



 0, 187510 = 0, 125 + 0, 0625
0, 187510 = 0, 125 + 0, 0625