Chapitre 04
Probabilités
Lors de l'inspection d'une scène de crime, la police scientifique recueille du
matériel génétique. Mais le rapport transmis aux enquêteur est incomplet.
Ils arrivent à lire les renseignements suivants :
- Les suspects ont soit des cheveux blonds, soit des cheveux chatains, soit des cheveux noirs.
- 40\% des suspects ont les cheveux blond.
- 10\% des suspects ont les cheveux châtain
- 60\% des suspects aux cheveux noir sont des femmes.
- 20\% du matériel génétique relevé provenant d'un individu aux cheveux blond est celui d'une femme.
- 70\% du matériel génétique relevé provenant d'un individu aux cheveux châtain est celui d'un homme.
Le criminel a-t-il plus de chance d'être un homme ou une femme ?
Pour trouver une réponse, il nous faut connaître :- La probabilité d'avoir une femme au cheveux noirs comme suspecte.
- La probabilité d'avoir un homme avec des cheveux châtains.
- Sachant que le suspect est une femme quelle est la probabilité qu'il ait les cheveux blonds ?
- Sachant que le suspect est un homme quelle est la probabilité qu'il ait des cheveux noirs ?
I. Quelques définitions & notations
Événement contraire
On appelle évènement contraire de A, on le note \overline{A} ( se lit A barre ), l'évènement constitué de toutes les issues de \Omega qui ne sont pas dans AExemple :
L'évènement \overline{F} est donc l'évènement contraire de F donc : être un homme.Intersection
On appelle intersection de A et de B, on le note A\cap B (se lit A inter B ), l'évènement constitué de toutes les issues qui sont commune à A et à BExemple :
L'évènement F \cap B est donc l'évènement : être une femme et avoir les cheveux blonds, donc les femmes blondes.Union
On appelle union de A et de B, on le note A\cup B (se lit A union B ), l'évènement constitué de toutes les issues de A ou de B.Exemple :
L'évènement C \cup B est donc l'évènement : avoir les cheveux châtains ou les cheveux blonds.Événements incompatibles
On appelle événements incompatibles, deux événements qui ne peuvent se produire en même tempsExemple :
L'évènement F\cap \overline{F} est donc l'évènement correspondant à l'ensemble des suspects étant à la fois des femmes et des hommes" soit F\cap \overline{F}=\emptyset.Probabilité
Intuitivement la probabilité d'un évènement A inclus dans un Univers \Omega est le rapport de la partie lié à A sur \Omega.Ainsi :
P(A)=\dfrac{\textbf{Nombre de cas favorables à \textit{A} }}{\textbf{Nombre de cas
possibles}}
Propriété
La probabilité d'un évènement est donc comprise entre 0 et 1.Exemple :
Ainsi dans l'activité précédente , quelle est la probabilité que le suspect soit une femme blonde.
P(\text{ Le suspect provient d'une femme aux cheveux blonds})
P(B \cap F) =\dfrac{\text{ Nombre de femmes blondes}}{\text{ Nombre total}}
P(B \cap F) =\dfrac{8}{100}
P(B \cap F) =\dfrac{\text{ Nombre de femmes blondes}}{\text{ Nombre total}}
P(B \cap F) =\dfrac{8}{100}
Probabilité conditionnelle
Notation : La probabilité de l'evenement A sachant que l'evenement B est réalisé se note :P_B(A) et se lit probabilité de A sachant B
P_B(A)= \dfrac{\text{Nombre de femmes blondes}}{\text{Nombre de femme}}= \dfrac{P(A \cap B) }{P(B)}
Exemple :
Ainsi dans l'activité précédente :P(\small \text{Le suspect est blonde sachant que c'est une femme })
P_F(B)= \dfrac{\text{ Nombre de femmes blondes}}{\text{ Nombre de femme}} = \dfrac{ 8 }{ 41 } = \dfrac{\frac{8}{100}}{\frac{41}{100}}
Probabilité de l'événement contraire
- P(\overline{A})= 1 - P(A)
Exemple
P(\text{ Le suspect est un homme})P(\overline{F}) = 1 - P(F) = 0,59
Arbre de probabilité
La construction d'un arbre de probabilité ( ou arbre pondéré ) répond à trois règles :- La somme des probabilité partant d'un même noeud est égale à 1.
- La probabilité d'un chemin est le produit de toutes les probabilités rencontrées sur les branches qui forment ce chemin .
- La probabilité d'un évènement est la somme des probabilités des chemins qui mènent à cet évènement.
Construction de l'arbre les experts
Rappels :
- P(B)= 0,4
- P(C) = 0,1
- P_{N}(F) = 0,6
- P_B(F) = 0,2
- P_C(\overline{F})=0,7
Exemple : Expert
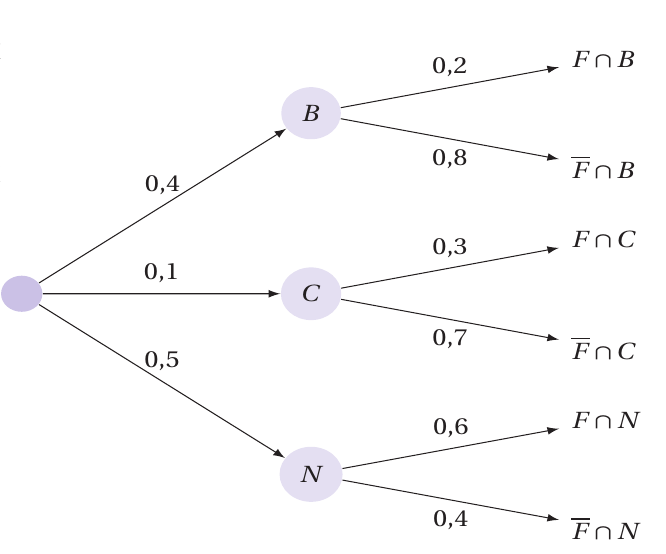
- Quelle est la probabilité que le coupable soit un homme sachant que ses cheveux sont blond ?
- Quelle est la probabilité que le coupable soit une femme aux cheveux noirs ?
Partition de l'univers
Soit \Omega un Univers de probabilité.On appelle partition de l'Univers un ensemble d'évènement A_1, A_2, .., A_n, où n\in\mathbb{N}^* tel que :
- L'union de tous les événements forme l'univers, soit A_1\cup A_2 \cup A_3 \cup..\cup A_{n-1}\cup A_n=\Omega
-
L'intersection de deux évènements quelconques de cet ensemble est vide.
Soit pour tout i et j A_i\cap A_j=\emptyset, avec 1\leq i,j\leq n
Probabilités totales
Soit A_1, A_2, .., A_n, où n\in\mathbb{N}^* une partition de l'Univers, alors :\small P(B) = P(A_1 \cap B) + P(A_2 \cap B) + ... + P(A_n \cap B)
Exercice 2 p294

Exercice 3 p294

Exercice 7 p294
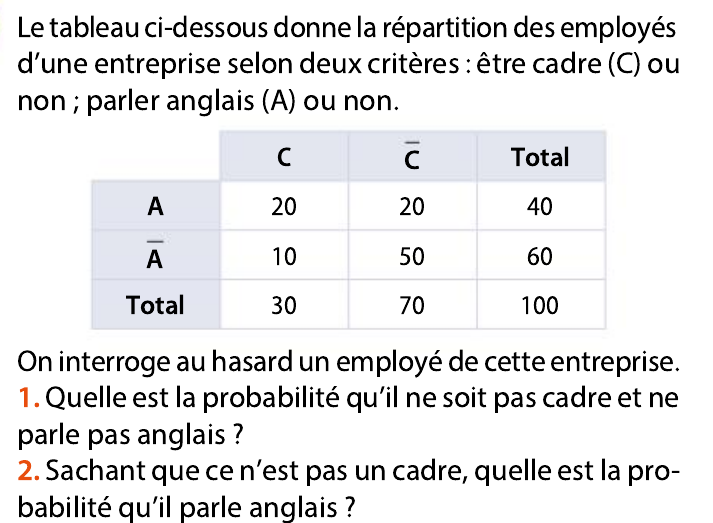
Exercice 8 p294

Exercice 18 p295

Exercice 40 p298

Exercice 58 p295 (Type 1)


Le jeu de monty hall
Evenements indépendants
A et B sont indépendants\displaystyle \Leftrightarrow \mathbb {P} (A\cap B)=\mathbb {P} (A)\times \mathbb {P} (B)
On a aussi l'équivalence A et B sont indépendants
\displaystyle \Leftrightarrow \mathbb {P}_B(A)=\mathbb {P} (A)
\displaystyle \Leftrightarrow \mathbb {P}_A(B)=\mathbb {P} (B)
Exercice 24 p296

Exercice 25 p296

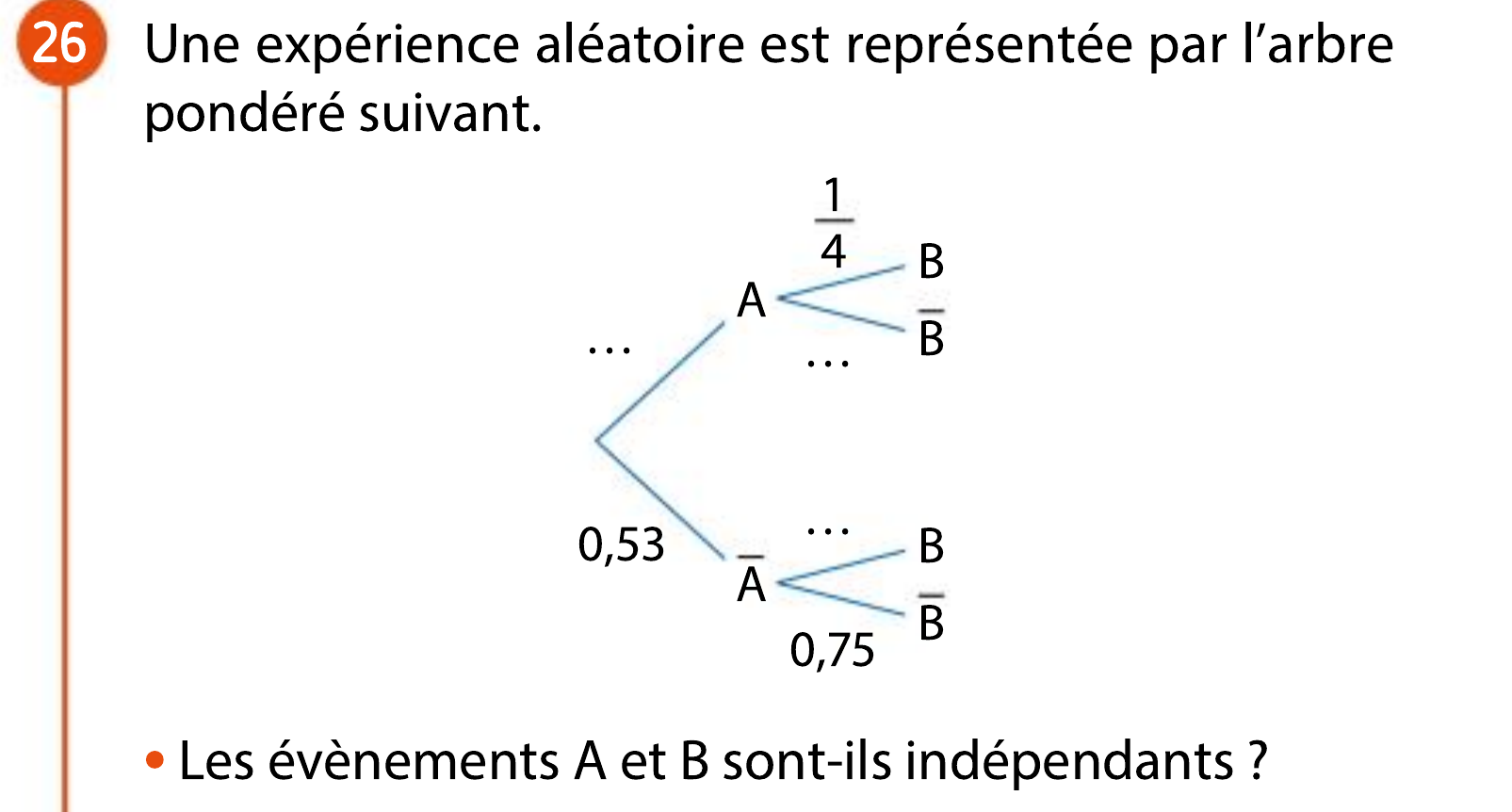
Exercice 26 p296
Exercice 28 p296

L'aiguille de Buffon (63 p295)


Exercices & méthodes videos
Exercice
Un laboratoire pharmaceutique a réalisé des tests sur 800 patients atteints d’une maladie bénigne. Certains sont traités avec le médicament A, d’autres avec le médicament B. Le tableau présente les résultats de l’étude| Médicament A | Médicament B | Total | |
|---|---|---|---|
| Guéri | 383 | 291 | 674 |
| Non guéri | 72 | 54 | 126 |
| Total | 455 | 345 | 800 |
- A : « Le patient a pris le médicament A. »
- G : « Le patient est guéri. »
- Calculer P_G(A) et P_A(G)
Exercice 2
On tire une carte au hasard dans un jeu de 32 cartes.- Soit A l'événement "Le résultat est un pique".
- Soit B l'événement "Le résultat est un roi". Donc A \cap B est l'événement "Le résultat est le roi de pique".
Un sac contient 50 boules, dont 20 boules rouges et 30 boules noires, où il est
marqué soit "Gagné" ou soit "Perdu"
Sur 15 boules rouges, il est mahttps://sorciersdesalem.math.cnrs.fr/Vulgarisation/Hall/hall.htmlrqué Gagné.
Sur 9 boules noires, il est marqué Gagné.
On tire au hasard une boule dans le sac.
Sur 15 boules rouges, il est mahttps://sorciersdesalem.math.cnrs.fr/Vulgarisation/Hall/hall.htmlrqué Gagné.
Sur 9 boules noires, il est marqué Gagné.
On tire au hasard une boule dans le sac.
- Soit R l'événement "On tire une boule rouge".
- Soit G l'événement "On tire une boule marquée Gagné"
- Calculer P(R)
Lors d’une épidémie chez des bovins, si la maladie est
diagnostiquée suffisamment tôt chez un animal, on peut le guérir ; sinon la maladie est mortelle.
Un test est mis au point et essayé sur un échantillon d’animaux dont 2 % est porteur de la maladie avec les
résultats suivants :
- si un animal est malade, le test est positif dans 85 % des cas ;
- si un animal est sain, le test est négatif dans 95 % des cas.
- Un animal est choisi au hasard. Quelle est la probabilité que son test soit positif ?
- Si le test du bovin est positif, quelle est la probabilité qu’il soit malade ?