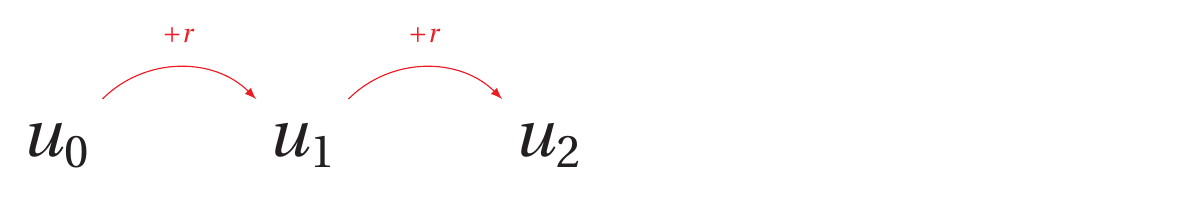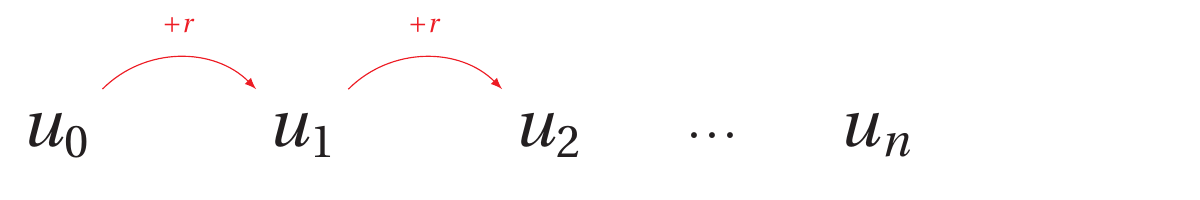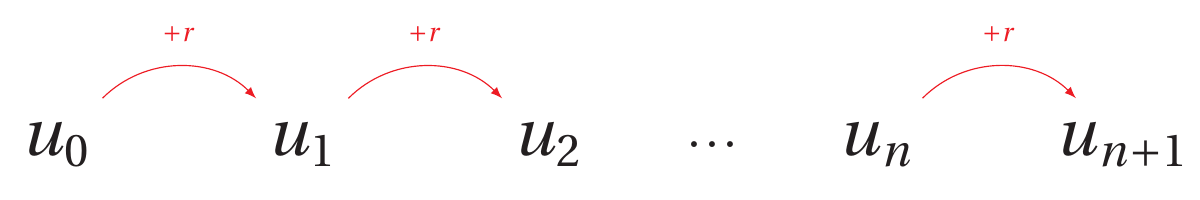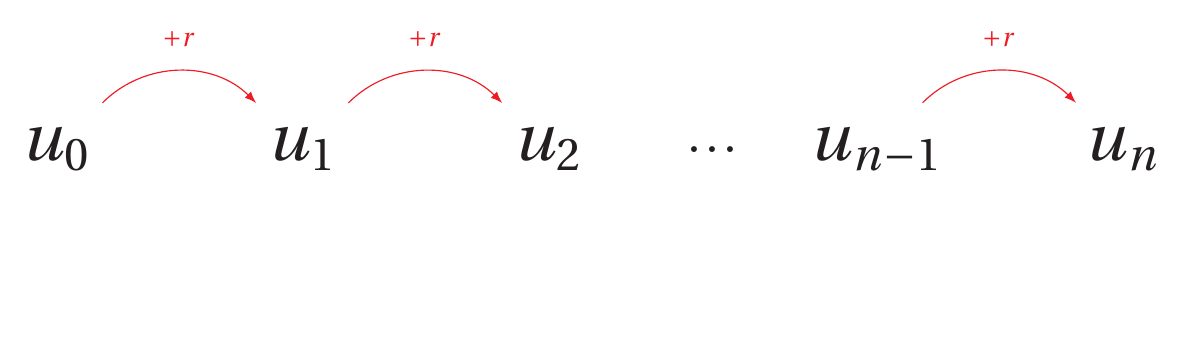Suites Numériques

Partie - B










T-Robert Malthus

Modélisation de la population et des ressources

T-Robert Malthus

Au cours de ces recherches, Thomas-Robert Malthus a travaillé sur l’évolution de la population en Angleterre.
En 1800, la population anglaise était de 8,3 millions d’habitants.
Bien que très pauvre en majorité, toute la population arrivait tant bien que mal à se nourrir.
Thomas Malthus prévoit que cette situation ne pourra pas durer au cours du temps. Il émet les hypothèses suivantes :
  • la population en Angleterre augmente chaque année de 2 % ;
  • la production agricole anglaise aidée par des avancées techniques, permet de nourrir 400 000 habitants de plus par an.


  1. Traduire les hypothèses de Thomas Malthus en choisissant deux suites (U_n) et (V_n).
    (U_n) représentant la population anglaise l'année 1800+ n et (V_n) la production agricole cette même année.
  2. En utilisant les hypothèses de Malthus, quelle est la population de l’Angleterre en 1801 et le nombre de personnes pouvant être nourries cette année-là ?
  3. La population anglaise pourra-elle suffisamment se nourrir en 1825 ?
  4. Selon ce modèle, pouvait-il craindre une famine en Angleterre ? Justifier.

Suites arithmétiques

La modélisation des ressources

Suites arithmétiques

Suites arithmétiques

Soit u_0 un nombre réel.
Une suite (u_n) de premier terme u_0 est arithmétique s’il existe un nombre réel r tel que, pour tout n entier naturel, on a u_{n+1} = u_n + r . Le nombre r est appelé raison de la suite (u_n).

Propriété : Forme explicite

Propriété : Forme explicite

Soit (u_n) une suite arithmétique de premier terme u_0 et de raison r, alors :
u_n = u_0 + r \times n
On a aussi :
u_n = u_1 + r \times ( n - 1 )
u_n = u_p + r \times ( n - p )

Étude d'une suite arithmétique.

Soit la suite (u _n) définie par u_0 = -7 et, pour tout entier naturel n, u_{n+1} = u_n + 4.
  • Donner la formule explicite de u_n . En déduire la valeur de u_{21}.
  • Un terme de la suite vaut-il 2019 ?

Suites géométriques

La modélisation de la population

Suite géométrique

Suite géométrique

Soit u_0 un nombre réel.
Une suite (u_n) de premier terme u_0 est géométrique s’il existe un nombre réel q tel que, pour tout n entier naturel, on a u_n = q \times u_n. Le nombre q est appelé raison de la suite (u_n).

Propriété : Forme explicite

Propriété : Forme explicite

Soit (u_n) une suite géométrique de premier terme u_0 et de raison q, alors :
u_n = u_0 \times q^n
On a aussi :
u_n = u_1 \times q^{( n - 1 )}
u_n = u_p \times q^{( n - p )}

Étude d'une suite géométrique.

Soit la suite (u_n) définie par u_0= 6 et, pour tout entier naturel n, u_{n+1} = \dfrac{3}{2}u_{n}.
  • Donner la formule explicite de u_n. En déduire la valeur exacte puis arrondie à l’unité de u_{11}.
  • Quel est le rang du premier terme qui dépasse 100 ?
Donner la relation entre u_{n+1} et u_n sachant qu’à chaque étape :
  1. on double ;
  2. u_n augmente de 3{,}5 ;
  3. u_n augmente de 15\,\% ;
  1. u_n diminue de 50 ;
  2. u_n diminue de 3\,\% ;
  3. u_n diminue de 12{,}4\,\%.


Dans chaque cas, indiquer s’il s’agit d’une suite arithmétique ou géométrique et donner la relation de récurrence. 
u = -4
for i in range(n):
    u = u + 3
v = 600
for i in range(n):
    v = 1.25 * v
w = 0
for i in range(n):
    w = i + 2 * v
  1. Indiquer le premier terme et la relation de récurrence de chacune de ces suites.
  2. Si possible, donner la nature de la suite.

Reconnaître parmi les suites suivantes celles qui sont arithmétiques, géométriques et préciser alors leur premier terme et leur raison.


  1. u_n = -2 + 3n.
  2. u_n = \dfrac{1}{2}n.
  3. u_n = n + \dfrac{5}{2}.
  4. u_n = \dfrac{3}{n}.
  1. u_n = 3n.
  2. u_n = 2n - 4.
  3. u_n = \dfrac{3n^2}{n}.
  4. u_n = 3n^2.

Forme explicite

Pour les suites arithmétiques suivantes, exprimer u_n en fonction de n puis calculer u_8.

  1. u_0 = 5 et r = 3.

  2. \left\lbrace \begin{array}{l} u_0 = 5 \\ u_{n+1} = u_n - 1 \end{array}\right.

  3. u_0 = 3 et r = \dfrac{1}{8}.
  1. \left\lbrace \begin{array}{l} u_0 = -2 \\ u_{n+1} = u_n + \dfrac{3}{2} \end{array}\right.
  2. \left\lbrace \begin{array}{l} u_0 = 3 \\ u_{n+1} = u_n + \dfrac{5}{4} \end{array}\right.
  3. u_1 = 1 et r = 2.

Forme explicite

Pour les suites géométriques suivantes (premier terme et raison donnés), exprimer u_n en fonction de n puis calculer u_5.
  1. u_0 = 3 et q = 2.
  2. u_0 = -5 et q = -1.
  3. u_0 = -2 et q = -3.
  1. \left\lbrace \begin{array}{l} u_0 = 10 \\ u_{n+1} = \dfrac{1}{2} u_n \end{array}\right.
  2. \left\lbrace \begin{array}{l} u_1 = 2 \\ u_{n+1} = 3 u_n \end{array}\right.

Variations des suites géométriques et arithmétiques

Représentation graphique

r \gt 0
r \lt 0

Propriété : Variation

Soit (u_n) une suite arithmétique de premier terme u_0 et de raison r.
  • Si r \lt 0 , alors (u_n) est décroissante
  • Si r = 0 , alors (u_n) est constante
  • Si r \gt 0 , alors (u_n) est croissante

Exercice

La suite (U_n) est définie, par :
\left\lbrace \begin{array}{l} U_0 =-1\\ U_{n+1} = u_n -5 \end{array} \right.

Déterminer la nature de la suite (U_n), son expression explicite, puis déterminer son sens de variation.

La suite (q^n)

Variation d'une suite géométrique

Pour une suite géométrique (u_n) de premier terme u_0 et de raison q :
  • si u_0 est positif, la suite (u_n) a le même sens de variation que la suite (q^n) ;
  • si u_0 est négatif, la suite (u_n) a le sens de variation contraire de celui de la suite (q^n).

Somme des n^{\text{ier}} entiers

Pour tout entier naturel n non nul, on a :
1 + 2 + 3 + ... + n = \dfrac{n(n+1)}{2}

Somme des n^{\text{ier}} entiers

De manière générale, la somme S de termes consecutifs d'une suite arithmétique est donnée par :

S = \text{Nombre de termes} \times \dfrac{ \text{Premier terme} + \text{Dernier terme}}{2}

Somme des q^n

Pour tout entier naturel n et pour tout réel q différent de 1, on a :
1 + q + q^2 + .... + q^n = \dfrac{1 - q^{n+1}}{1-q}

Démonstration

Somme des premiers termes d'une suite géométrique

Soit U_n une suite géométrique, alors la somme des premiers termes consécutifs d'une suite gémétrique est donnée par :

U_0 + ... + U_n = U_0 \times \dfrac{1 - q^{n+1}}{1-q}

Exercice

Démontrer la propriété précédente.

Généralisation

De manière générale, la somme des termes consécutifs d'une suite géométrique de raison q est donnée par :

S = \text{Premier terme} \times \dfrac{1 - q^{\text{Nombre de termes}}}{1-q}

Exercice 58 p.35

Exercice 57 p.35