Suites

Partie A

Objectifs :

Connaître et utiliser les différents mode de génération d'une suite
Etudier les variations d'une suite
Conjecturer la limite d'une suite

Ainsi de suite ....

Pour chacune des suites de nombres ci-dessous, déterminer le nombres suivants :

1, 3, 5, 7, ...

1, 4, 9, 16, 25, ...

2, 3, 5, 7, 11, 13, ...

1, 1, 2, 3, 5, 8, 13, ...

1, 11, 21, 1211, 3112, ...

Etape 0

suite numérique

Une suite numérique est une liste ordonnée de nombres réels telle qu'à tout entier $n$ on associe un nombre réel noté $u_n$ .
$u_n$ (se lit « u indice n ») est appelé le terme de rang $n$ de cette suite (ou d'indice $n$ ).

On peut lui associer une fonction définie sur $\mathbb{N}$ par $u$ :
$\mathbb{N} \longrightarrow \mathbb{R}$
$n \longrightarrow u(n) = u_n$
On note cette suite $(u_n )$ .

Exercice

La liste 50 ; 25 ; 12,5 ; 6,25 ...
définit les premiers termes de la suite $(U_n)$ telle que $U_0 = 50$

Déterminer :

$U_2$ = ...
$U_4$ = ...

Exercice

La liste 2 ; 4 ; 6 ; 8 ...
définit les premiers termes de la suite $(V_n)$ telle que $V_1 = 2$
Déterminer :

$V_2$ = ...
$V_6$ = ...

Forme explicite $u_n = f(n)$

Une suite est définie par une formule explicite lorsque $u_n$ s’exprime en fonction de l’entier $n$ .
Dans ce cas, on peut calculer chaque terme directement à partir de rang $n$ .

Exercice

Pour tout entier naturel $n$ , on donne $U_n = 2n$ .
Calculer $U_0, U_3, U_{10}$ .
Pour tout entier naturel $n \geq 1$ , on donne $V_n = \sqrt{n- 1}$ . Calculer $V_1, V_3, V_{10}$ .

Exercice 1 p.30

Suite définie par récurrence

Une suite est définie par une relation de récurrence lorsqu’elle est définie par la donnée de :

son premier terme ;
une relation qui permet de calculer chaque terme à partir du précédent, $u_{n+1} = f(u_n)$ .

Dans ce cas, pour calculer chaque terme

u_n

, il faut avoir calculé tous les termes qui le précèdent.

Exercice :

On définit la suite $(U_n )$ par $U_0 = 5$ et chaque terme est le triple de son précédent;
On définit la suite $(V_n )$ par $V_0 = 3$ et $V_{n+1} = 4V_n - 6$ ;

Pour chacune des suites ci-dessus, calculer les 4 premiers termes.

Exercice — Calcul de termes

Soit $(U_n)$ définie par $U_n = 2n^2 - 1$ .
Calculer $U_0$ , $U_1$ et $U_5$ .
Soit $(V_n)$ définie par $V_n = \dfrac{n+1}{n}$ .
Calculer $V_1$ et $V_5$ .
Soit $(W_n)$ définie par :
$\begin{cases} W_0 = 3, \\\\ W_{n+1} = 4W_n + 2 \end{cases}$ Calculer $W_1$ , $W_2$ et $W_4$ .

Exercice — Algorithme (Python)

On considère les trois fonctions Python suivantes :

def terme_u(n):
    u = 3
    for k in range(n):
        u = 2*u + 3
    return u

def terme_v(n):
    return n**2 + 3*n + 1

def terme_w(n):
    u = 3
    for k in range(n):
        u = 1/u - 1
    return u

Qu’obtient-on pour terme_u(5), terme_v(4) et terme_w(3) ?

Exercice — Bactéries

Une solution contient 5000 bactéries à l’instant $n=0$ . À chaque minute la population augmente de 15% et 100 bactéries meurent.

Calculer $U_1$ puis $U_2$ .
Exprimer $U_{n+1}$ en fonction de $U_n$ .
Compléter le programme :

def seuil():
    n = 0
    u = 5000
    while u <= .......:
        n = ........
        u = ........
    return ......

Exercice — Démontrer

Soit $U_n = (n+2)^2$ et $V_{n+1} = V_n + 2n + 5$ avec $V_0=4$ .

Calculer $U_0,U_1,U_2,U_3$ et $V_1,V_2,V_3$ .
Conjecturer une relation entre $U_n$ et $V_n$ .
Démontrer la conjecture.

Exercice — Démontrer

Soit $U_n = (n+2)^2$ et $V_{n+1} = V_n + 2n + 5$ avec $V_0=4$ .

Calculer $U_0,U_1,U_2,U_3$ et $V_1,V_2,V_3$ .
Conjecturer une relation entre $U_n$ et $V_n$ .
Démontrer la conjecture.

Variations

On dit qu'une suite $(U_n)$ est croissante lorsque pour tout $n\in\mathbb{N}$ , $U_n \leq U_{n+1}$ .

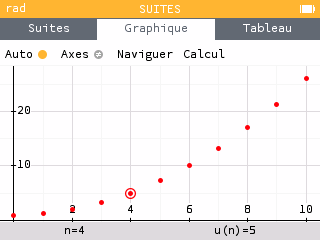
On dit qu'une suite $(U_n)$ est décroissante lorsque pour tout $n\in\mathbb{N}$ , $U_n \geq U_{n+1}$ .

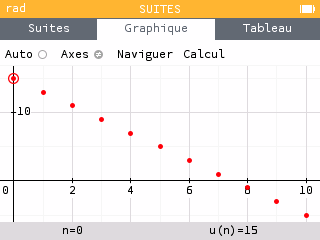
On dit qu'une suite $(U_n)$ est constante lorsque pour tout $n\in\mathbb{N}$ , $U_n = U_{n+1}$ .

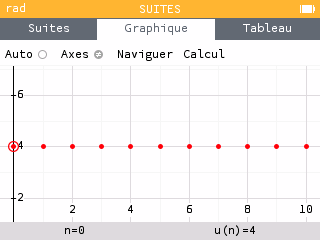
On dit qu'une suite est monotone, lorsqu'elle est toujours croissante ou toujours décroissante.
On dira qu'une suite est strictement croissante ou strictement décroissante, si les inégalités sont strictes.

Méthode 1

Pour déterminer les variations d'une suite, on étudie le signe de la différence

U_{n+1} - U_n

Si $U_{n+1} - U_n \geq 0$ , la suite $U_n$ est croissante.
Si $U_{n+1} - U_n \leq 0$ , la suite $U_n$ est décroissante.
Si $U_{n+1} - U_n = 0$ , la suite $U_n$ est constante.

Méthode 2

(U_n)

est une suite strictement positive, on peut comparer le quotient

\dfrac{U_{n+1}}{U_n}

à 1

Si $\dfrac{U_{n+1}}{U_n} \geq 1$ , la suite $U_n$ est croissante.
Si $\dfrac{U_{n+1}}{U_n} \leq 1$ , la suite $U_n$ est décroissante.
Si $\dfrac{U_{n+1}}{U_n} = 1$ , la suite $U_n$ est constante.

Méthode 3

(U_n)

est définie de manière explicite par

U_n = f(n)

on peut utiliser les variations de

f

Si $f$ est croissante, la suite $U_n$ est croissante.
Si $f$ est décroissante, la suite $U_n$ est décroissante.
Si $f$ est constante, la suite $U_n$ est constante.

Exercice — Lecture graphique

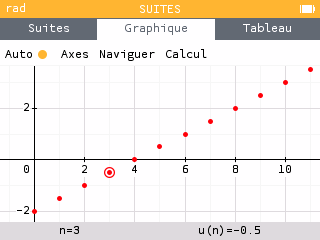
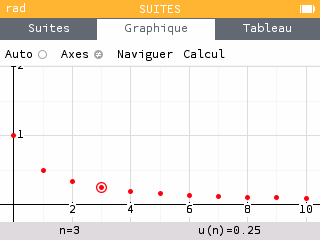
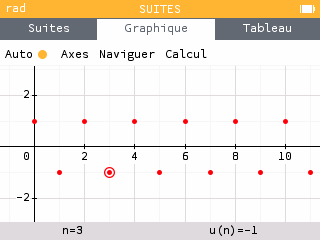
Exercice — Conjecture

Soit $U_n = (n+1)(n-11)$ .

Calculer $U_0\ldots U_4$ .
Conjecturer les variations.
Calculer $U_{10}$ et conclure.

Exercice — Savoir-faire 2

Montrer que $U_n = n^2 + 3n - 5$ est croissante.
Avec $V_{n+1} = V_n - n^2, V_0=3$ , montrer que $(V_n)$ est décroissante.

Exercice — Étude de $U_n = n - 1/n$

Étudier les variations de $U_n$ sur $\\mathbb{N}^*$ .

Exercice — Trois suites

Déterminer le sens de variation des suites définies sur

\mathbb{N}^*

par les formules suivantes :

$U_n = 3 - 6n$
$V_n = n^2$
$W_n = 1/n$

Déterminer leur sens de variation.

Exercice

Étudier les variations de

U_n = \dfrac{2^n}{7n}

SF2 (Entraînement)

$U_n = n^2+n$ .
Montrer que $(U_n)$ est croissante.

SF2 (Entraînement)

$V_n = \dfrac{n+3}{n+1}$ .
Déterminer le sens de variation.

SF2 (Approfondissement)

$W_n = 3^n - n$ .

Déterminer le sens de variation.

SF2 (Approfondissement)

X_0=2,\\quad X_{n+1}=X_n - \dfrac{1}{(n+1)^2}

Montrer que la suite est décroissante.

Le problème de Yoyo

Notion de limite

Balle rebondissante

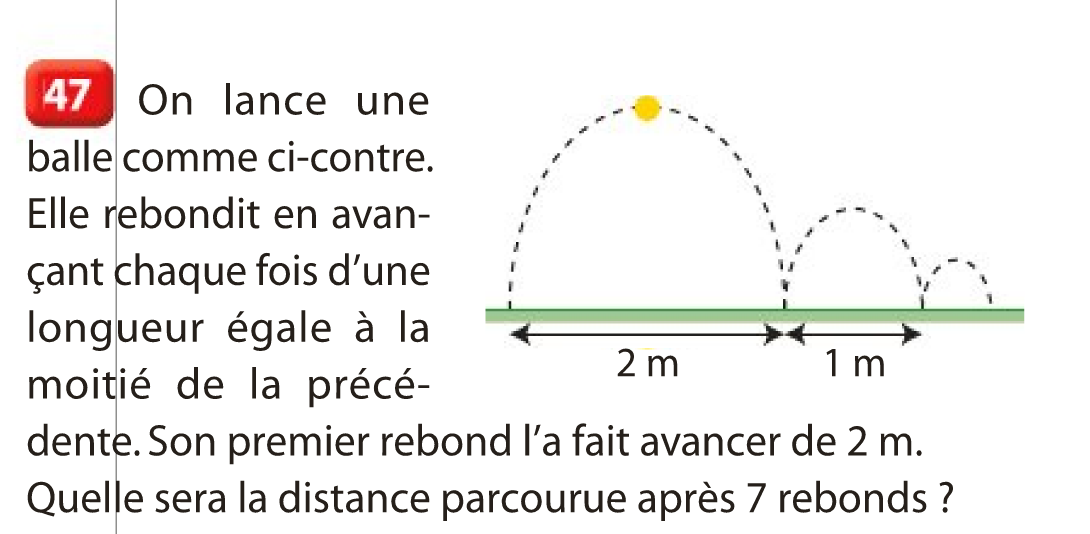Au bout de combien de rebonds, la balle aura-t-elle parcourus :

3,80 m ?
3,99 m ?
4,50 m ?

Limite finie

Lorque les termes

u_n

semblent tous se rapprocher autant que l’on veut d’un nombre

k

.
On dit que la suite

(u_n)

tend vers

k

lorsque

n

tend vers

+\infty

Notation :

\displaystyle{\lim_{n\to +\infty} u_n = k}

Représentation graphique

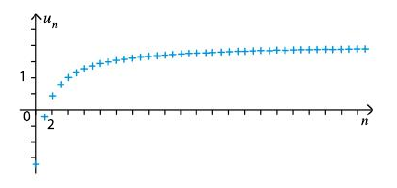
Limite infinie

Lorque les termes

u_n

semblent devenir aussi grands que l’on veut.
On dit que la suite

(u_n)

tend vers plus l'infinie lorsque

n

tend vers plus l'infinie

Notation :

\displaystyle{\lim_{n\to +\infty} u_n = + \infty}

Limite infinie

Lorque les termes

u_n

semblent devenir aussi petits que l’on veut.
On dit que la suite

(u_n)

tend vers moins l'infinie lorsque

n

tend vers plus l'infinie

Notation :

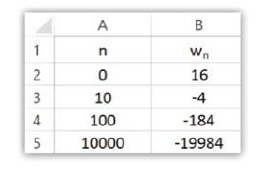
\displaystyle{\lim_{n\to +\infty} u_n = - \infty}

Remarques

Certaines suite n'admet pas de limite.
Par exemple la suite

(u_n)

définie par

u_n = (-1)^n

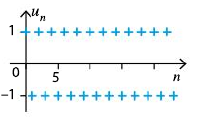
Exercice

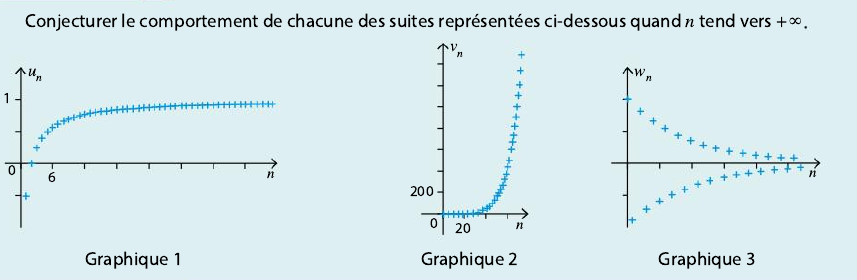
Exercice 45p.33

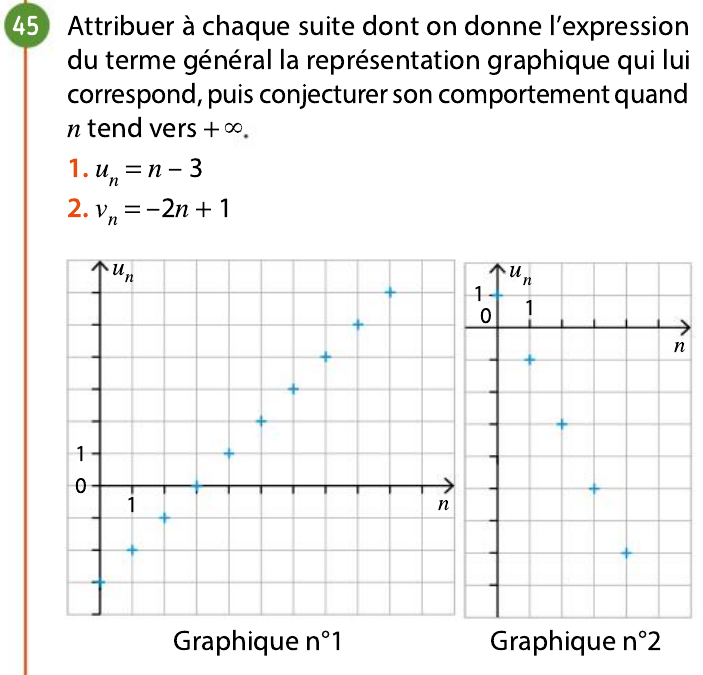
Exercice 46p.33

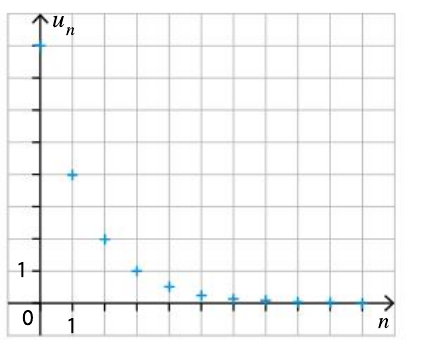
Conjecturer la limite de la suite $(u_n)$ repéresentée sur le graphique ci-dessus.

Suites

Partie A

Ainsi de suite ....

suite numérique

Exercice

Exercice

Forme explicite u_n = f(n)

Exercice

Exercice 1 p.30

Exercice 1 p.30

Suite définie par récurrence

Exercice :

Exercice — Calcul de termes

Exercice — Algorithme (Python)

Exercice — Bactéries

Exercice — Démontrer

Exercice — Démontrer

Variations

Méthode 1

Méthode 2

Méthode 3

Exercice — Lecture graphique

Exercice — Conjecture

Exercice — Savoir-faire 2

Exercice — Étude de U_n = n - 1/n

Exercice — Trois suites

Exercice

SF2 (Entraînement)

SF2 (Entraînement)

SF2 (Approfondissement)

SF2 (Approfondissement)

Le problème de Yoyo

Notion de limite

Balle rebondissante

Limite finie

Représentation graphique

Limite infinie

Limite infinie

Remarques

Exercice

Exercice 45p.33

Exercice 46p.33

Forme explicite $u_n = f(n)$

Exercice — Étude de $U_n = n - 1/n$